Bài tập 18 trang 135 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
Đề bài
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
Lời giải chi tiết
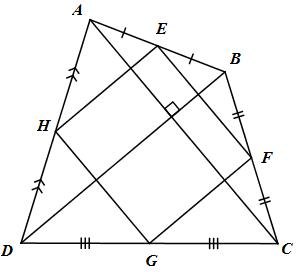
E, F lần lượt là trung điểm của AB và BC.
\( \Rightarrow EF\) là đường trung bình của tam giác ABC \( \Rightarrow EF//AC\) và \(EF = {1 \over 2}AC\,\,\,\left( 1 \right)\)
H, G lần lượt là trung điểm của AD và CD
\( \Rightarrow HG\) là đường trung bình của tam giác ACD \( \Rightarrow HG//AC\) và \(HG = {1 \over 2}AC\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra EF // HG và \(EF = HG\)
Vậy tứ giác HEFG là hình bình hành.
G, F lần lượt là trung điểm của DC và BC
\( \Rightarrow GF\) là đường trung bình của tam giác BDC.
\( \Rightarrow GF//BD\)
Mà \(BD \bot AC\,\,\left( {gt} \right)\) nên \(GF \bot AC\)
Ta có \(GF \bot AC,\,\,EF//AC \Rightarrow GF \bot EF \Rightarrow \widehat {EFG} = {90^0}\)
Hình bình hành HEFG có \(\widehat {EFG} = {90^0}\) nên là hình chữ nhật.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 18 trang 135 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"