Bài 9 trang 59 SGK Toán 7 tập 2
Giải bài 9 trang 59 SGK Toán 7 tập 2. Để tập bơi nâng dần khoảng cách,
Đề bài
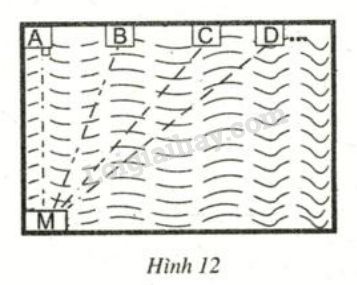
Để tập bơi nâng dần khoảng cách, hàng ngày bạn Nam xuất phát từ \(M\), ngày thứ nhất bạn bơi đến \(A\), ngày thứ hai bạn bơi đến \(B\), ngày thứ ba bạn bơi đến \(C\) ...(hình 12).
Hỏi rằng bạn Nam tập bơi như thế có đúng mục đích đề ra hay không (ngày hôm sau có bơi xa hơn ngày hôm trước hay không)? Vì sao?
Phương pháp giải - Xem chi tiết
Áp dụng định lí về quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
Lời giải chi tiết
Theo hình vẽ các điểm \(A, B, C, D\) nằm trên một đường thẳng (ta gọi là đường thẳng \(d \)) và điểm \(M\) nằm ngoài đường thẳng đó. \(MA\) là đường vuông góc kẻ từ \(M\) đến đường thẳng \(d\). Các đoạn thẳng \(MB, MC, MD\) là các đường xiên kẻ từ \(M\) lần lượt đến \(B, C\) và \(D\).
Ta có \(AB, AC, AD\) lần lượt là hình chiếu của \(MB, MC, MD\) xuống \(d\).
Từ hình vẽ ta có \( AD > AC > AB \) suy ra \(MD > MC >MB \) (Theo định lí 2: đường xiên nào có hình chiếu lớn hơn thì lớn hơn) (1)
Theo định lí 1 đường vuông góc là đường ngắn nhất nên \(MA<MB\) (2)
Từ (1) và (2) suy ra: \(MD > MC >MB >MA\).
Điều đó có nghĩa là ngày hôm sau bạn Nam bơi được xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 9 trang 59 SGK Toán 7 tập 2 timdapan.com"







