Bài 11 trang 60 SGK Toán 7 tập 2
Giải bài 11 trang 60 SGK Toán 7 tập 2. Cho hình :Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh rằng
Đề bài
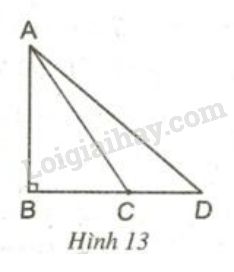
Cho hình \(13\): Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh rằng:
Nếu \(BC < BD\) thì \(AC < AD\)
Hướng dẫn:
a) Góc \(ACD\) là góc gì? Tại sao?
b) Trong tam giác \(ACD\), cạnh nào lớn nhất, tại sao?
Phương pháp giải - Xem chi tiết
Áp dụng quan hệ giữa góc và cạnh đối diện trong một tam giác.
Lời giải chi tiết
a) \(\widehat{ACD}\) là góc ngoài tại \(C\) của \(∆ABC\) nên \(\widehat{ACD}=\widehat{ABC}+\widehat{BAC}\)
Do đó \(\widehat{ACD}> \widehat{ABC}\).
Mà \(\widehat {ABC} = {90^o}\) tức là \(\widehat{ACD}>{90^o}\) hay \(\widehat{ACD}\) là góc tù.
b) Trong tam giác \(ACD\) có \(\widehat{ACD}\) là góc tù
Mà AD là cạnh đối diện với góc ACD.
Suy ra AD là cạnh lớn nhất trong tam giác ACD (cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác).
Nên AD > AC hay AC < AD
Vậy Nếu : BC < BD thì AC < AD.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 11 trang 60 SGK Toán 7 tập 2 timdapan.com"







