Bài 8.46 trang 90 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AC = a, BC = \(\sqrt 2 \)a, SA vuông góc với mặt phẳng đáy và SA = a.
Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AC = a, BC = \(\sqrt 2 \)a, SA vuông góc với mặt phẳng đáy và SA = a. Góc giữa đường thẳng SB và mặt phẳng đáy bằng
A. 600.
B. 900.
C. 300.
D. 450.
Phương pháp giải - Xem chi tiết
Góc giữa d và (P):
+ Tìm giao điểm O của d và (P).
+ Từ A bất kì trên d, kẻ đường thẳng AA’ vuông góc xuống (P).
+ Góc AOA’ là góc cần tìm.
Lời giải chi tiết
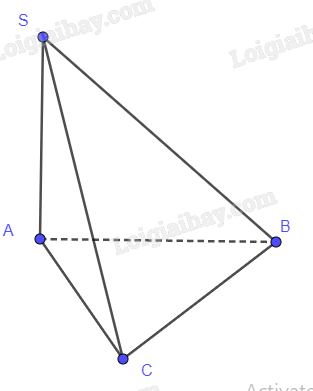
Góc giữa đường thẳng SB và mặt phẳng đáy là \(\widehat {SBA}\)
\(AB = \sqrt {A{C^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {\sqrt 2 a} \right)}^2}} = \sqrt 3 a\)
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {SBA} = {30^0}\)
Chọn đáp án C.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 8.46 trang 90 SGK Toán 11 tập 2 - Cùng khám phá timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 8.46 trang 90 SGK Toán 11 tập 2 - Cùng khám phá timdapan.com"







