Bài 82 trang 155 SGK Đại số 10 nâng cao

Giải các bất phương trình sau:

LG a

\({{x - 2} \over {{x^2} - 9x + 20}} > 0\)

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}x - 2 = 0 \Leftrightarrow x = 2\\{x^2} - 9x + 20 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 5\end{array} \right.\end{array}\)

Bảng xét dấu:

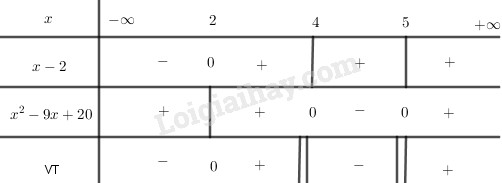
Từ bảng xét dấu ta có \(S = (2, 4) ∪ (5, +∞)\)

LG b

\({{2{x^2} - 10x + 14} \over {{x^2} - 3x + 2}} \ge 1\)

Lời giải chi tiết:

Bất phương trình đã cho tương đương với bất phương trình:

\({{2{x^2} - 10x + 14} \over {{x^2} - 3x + 2}} - 1 \ge 0\)

\(\begin{array}{l}
\Leftrightarrow \frac{{2{x^2} - 10x + 14 - {x^2} + 3x - 2}}{{{x^2} - 3x + 2}} \ge 0\\
\Leftrightarrow \frac{{{x^2} - 7x + 12}}{{{x^2} - 3x + 2}} \ge 0
\end{array}\)

Ta có:

\(\begin{array}{l}
{x^2} - 7x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 3\\
x = 4
\end{array} \right.\\
{x^2} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x = 2
\end{array} \right.
\end{array}\)

Bảng xét dấu:

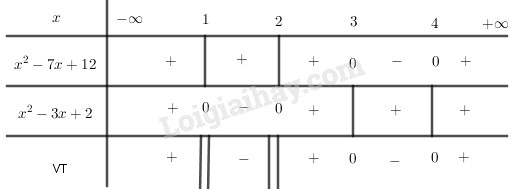
Tập nghiệm của bất phương trình đã cho là:

\(S = (-∞, 1) ∪ (2, 3] ∪ [4, +∞)\)