Bài 8 trang 222 SGK Đại số 10 Nâng cao

Biện luận theo tham số m số nghiệm và dấu các nghiệm của phương trình

LG a

x² + 4(m + 3)x + 6(m² – 5m + 6) = 0

Giải chi tiết:

Ta có:

Δ’ = 4(m + 3)² – 6(m² – 5m + 6) = -2m² + 54m

S = 4(m + 3); P = 6(m² – 5m + 6)

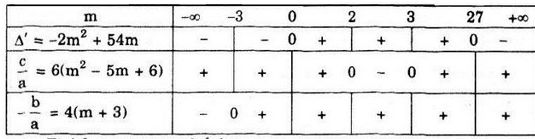
Bảng trên dẫn đến kết luận sau:

+ Nếu m < 0 hoặc m > 27 thì Δ’ < 0 nên phương trịnh vô nghiệm.

+ Nếu m = 0 hoặc m = 27 thì \(\Delta ' = 0;\,\,{c \over a} > 0;\,\, - {b \over a} > 0\) nên phương trình có một nghiệm dương (nghiệm kép)

+ Nếu 0 < m < 2  hoặc 3 < m < 27 thì \(\Delta ' > 0;\,\,{c \over a} > 0;\,\, - {b \over a} > 0\) nên phương trình có hai nghiệm dương phân biệt.

+ Nếu 2 < m < 3 thì \({c \over a} < 0\) nên phương trình có hai nghiệm trái dấu.

+ Nếu m = 2 hoặc m = 3 thì \({c \over a} = 0\,\,;{{ - b} \over a} > 0\) nên phương trình có một nghiệm bằng 0 và một nghiệm dương.

LG b

(m – 1)x² – (m – 3)x – m – 3 = 0

Giải chi tiết:

Khi m = 1, ta có phương trình 2x – 4 = 0. Phương trình có một nghiệm dương.

Khi m ≠ 1, ta có phương trình bậc hai. Số nghiệm và dấu của các nghiệm phụ thuộc vào dấu của các biểu thức sau:

\(\eqalign{
& \Delta = {(m - 3)^2} + 4(m - 1)(m + 3) \cr&= 5{m^2} + 2m - 3 \cr 
& P = {c \over a} = {{ - m - 3} \over {m - 1}} \cr 
& S = - {b \over a} = {{m - 3} \over {m - 1}} \cr} \) 

Ta có bảng xét dấu:

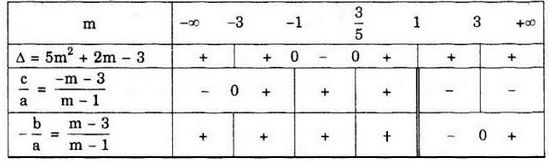
Từ bảng xét dấu, ta suy ra:

+ Nếu \( - 1 < m < {3 \over 5}\) thì Δ < 0 nên phương trình vô nghiệm

+ Nếu m < -3 hoặc m > 1 thì \({c \over a} < 0\) nên phương trình có hai nghiệm trái dấu.

+ Nếu -3 < m < -1 hoặc \({3 \over 5} < m < 1\) thì \(\Delta  > 0;\,{c \over a} > 0;\,{{ - b} \over a} > 0\) nên phương  trình có hai nghiệm dương phân biệt.

+ Nếu m = -3 thì \(\,{c \over a} = 0;\,{{ - b} \over a} > 0\) nên phương trình có một nghiệm x = 0, nghiệm kia là nghiệm  dương

+ Nếu m = -1 hoặc \(m = {3 \over 5}\) thì \(\Delta  = 0;\,{c \over a} > 0;\,{{ - b} \over a} > 0\) nên phương trình có một nghiệm kép dương.