Bài 7 trang 27 SGK Hình học 10

Đề bài

Các điểm \(A'(-4; 1), B'(2;4), C'(2, -2)\) lần lượt là trung điểm của các cạnh \(BC, CA\) và \(AB\) của tam giác \(ABC\). Tính tọa độ đỉnh của tam giác \(ABC\). Chứng minh rằng trọng tâm tam giác \(ABC\) và \(A'B'C'\) trùng nhau.

Lời giải chi tiết

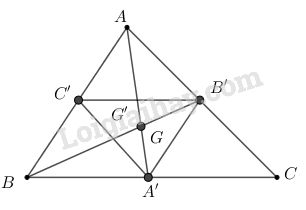
Giả sử \(A({x_A};{y_A}),B({x_B};{y_B}),C({x_C};{y_C})\)

\(A'\) là trung điểm của cạnh \(BC\) nên \(-4 = \frac{1}{2} (x_B+ x_C)\)

\(\Rightarrow {x_B} + {x_C} =  - 8\)                       (1)

Tương tự ta có \({x_A} + {x_C} = 4\)       (2)

                       \({x_B} + {x_A} = 4\)         (3)  

Giải hệ (1), (2) và (3) ta được:

       \(\left\{ \matrix{
{x_A} = 8 \hfill \cr
{x_B} = - 4 \hfill \cr
x{}_C = - 4 \hfill \cr} \right.\)

Tương tự ta tính được:

      \(\left\{ \matrix{
{y_A} = 1 \hfill \cr
{y_B} = - 5 \hfill \cr
y{}_C = 7 \hfill \cr} \right.\)

Gọi \(G({x_G};y{}_G)\) là trọng tâm của tam giác \(ABC\)

Khi đó ta có:

$$\left\{ \matrix{
{x_G} = {{{x_A} + {x_B} + {x_C}} \over 3} = {{8 - 4 - 4} \over 3} = 0 \hfill \cr
{y_G} = {{{y_A} + {y_B} + y{}_C} \over 3} = {{1 - 5 + 7} \over 3} = {1} \hfill \cr} \right.$$ 

Vậy \(G(0;1)\)  (*)

Gọi \(G'({x_{G'}};y{}_{G'})\) là trong tâm của tam giác \(A'B'C'\)

Khi đó ta có:

$$\left\{ \matrix{
{x_{G'}} = {{{x_{A'}} + {x_{B'}} + {x_{C'}}} \over 3} = {{ - 4 + 2 + 2} \over 3} = 0 \hfill \cr
{y_{G'}} = {{{y_{A'}} + {y_{B'}} + y{}_{C'}} \over 3} = {{1 + 4 - 2} \over 3} = 1 \hfill \cr} \right.$$

Vậy \(G'(0;1)\)  (2*)

Từ (*) và (2*) ta thấy \(G \equiv G'\)

Vậy trọng tâm tam giác \(ABC\) và \(A'B'C'\) trùng nhau.