Bài 6 trang 40 SGK Hình học 10
Giải bài 6 trang 40 SGK Hình học 10. Cho hình vuông ABCD
Đề bài
Cho hình vuông \(ABCD\). Tính: \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right), \, \sin\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right),\)\(\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right).\)
Phương pháp giải - Xem chi tiết
Cho hai vecto \(\overrightarrow a ,\;\overrightarrow b (khác \overrightarrow 0). \) Từ một điểm \(O\) bất kì ta vẽ \(\overrightarrow {OA} = \overrightarrow a ,\;\overrightarrow {OB} = \;\overrightarrow b .\)
Khi đó \(\widehat {AOB}\) với số đo từ \(0^0\) đến \(180^0\) được gọi là góc giữa hai vecto \(\overrightarrow a ,\;\overrightarrow b. \)
Kí hiệu: \(\left( {\overrightarrow a ,\;\overrightarrow b } \right).\)
Lời giải chi tiết
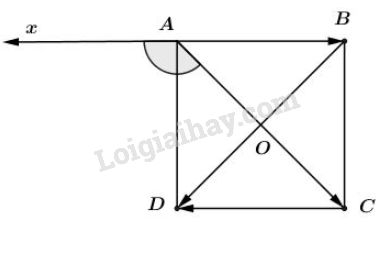
Ta có :
\( \eqalign{
& \cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) =\cos \widehat{CAx} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \cos {135^0} = {{\sqrt 2 } \over 2}, \cr & \sin\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right) =\sin \widehat{COD}\cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \sin {90^0} = 1, \cr & \cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \cos {180^0} =- 1 .\cr} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6 trang 40 SGK Hình học 10 timdapan.com"







