Bài 48 trang 135 SGK Đại số 10 nâng cao

Bài toán vitamin.

Một nhà khoa học nghiên cứ về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. kết quả như sau:

i) Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.

ii) Một người mỗi ngày cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B.

iii) Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn 1/2 số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A.

Giả sử x và y lần lượt là số đơn vị vitamin A và B mà bạn dùng mỗi ngày

LG a

Gọi c là số tiền vitamin mà bạn phải trả (tính bằng đồng). Hãy viết phương trình biểu diễn c dưới dạng một biểu thức của x và y, nếu giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng.

Lời giải chi tiết:

x đơn vị vitamin A giá 9x đồng.

y đơn vị vitamin B giá 7,5y đồng.

Vậy \(c = 9x + 7,5y\).

LG b

Viết các phương trình biểu thị i), ii) và iii), lập thành một hệ bất phương trình rồi biểu diễn miền nghiệm của hệ bất phương trình đó.

Lời giải chi tiết:

i) Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên

\(\left\{ \begin{array}{l}
0 \le x \le 600\\
0 \le y \le 500
\end{array} \right.\)

ii) Một người mỗi ngày cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B nên \(400 \le x + y \le 1000\).

iii) Số đơn vị vitamin B không ít hơn 1/2 số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A nên \(\frac{1}{2}x \le y \le 3x\).

Hệ phương trình nhận được là:

\(\left\{ \matrix{
0 \le x \le 600 \hfill \cr 
0 \le y \le 500 \hfill \cr 
400 \le x + y \le 1000 \hfill \cr 
{1 \over 2}x \le y \le 3x \hfill \cr} \right.\) 

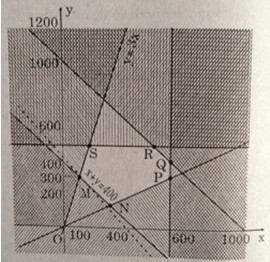
Miền nghiệm trên là miền đa giác MNPQRS (kể cả biên trên hình)

LG c

Tìm phương án dùng hai loại vitamin A và B thỏa mãn các điều kiện trên để số tiền phải trả là ít nhất, biết rằng c đạt giá trị nhỏ nhất tại một trong các đỉnh của miền nghiệm (S).

Lời giải chi tiết:

Ta có: \(M\left( {100;300} \right),N\left( {\frac{{800}}{3};\frac{{400}}{3}} \right),\) \(P\left( {600;300} \right),Q\left( {600;400} \right),\) \( R\left( {500;500} \right),S\left( {\frac{{500}}{3};500} \right)\)

\(\begin{array}{l}
c\left( M \right) = 9.100 + 7,5.300 = 3150\\
c\left( N \right) = 9.\frac{{800}}{3} + 7,5.\frac{{400}}{3} = 3400\\
c\left( P \right) = 9.600 + 7,5.300 = 7650\\
c\left( Q \right) = 9.600 + 7,5.400 = 8400\\
c\left( R \right) = 9.500 + 7,5.500 = 8250\\
c\left( S \right) = 9.\frac{{500}}{3} + 7,5.500 = 5250
\end{array}\)

Số tiền đạt giá trị nhỏ nhất tại \(M(100, 300)\) nên phương án tốt nhất là dùng 100 đơn vị vitamin A và 300 đơn vị vitamin B mỗi ngày.

Chi phí mỗi ngày là 3150 đồng.