Bài 47 trang 93 SGK Toán 8 tập 1

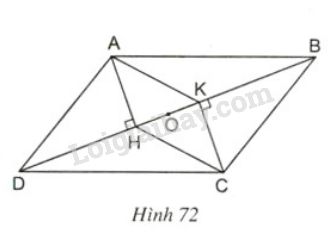
Cho hình \(72\), trong đó \(ABCD\) là hình bình hành.

LG a.

Chứng minh rằng \(AHCK\) là hình bình hành.

Phương pháp giải:

Áp dụng: Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Lời giải chi tiết:

Xét hai tam giác vuông \(AHD\) và \(CKB\) có:

    +) \( AD = CB\) (vì \(ABCD\) là hình bình hành)

    +) \(\widehat {ADH} = \widehat {CBK}\) (hai góc ở vị trí so le trong)

\( \Rightarrow \) \(∆AHD =  ∆CKB\) (cạnh huyền- góc nhọn)

\( \Rightarrow \) \(AH = CK\) (\(2\) cạnh tương ứng)

Ta có:

\(\left\{ \begin{array}{l}
AH \bot B{\rm{D}}\\
CK \bot B{\rm{D}}
\end{array} \right.\left( \text{giả thiết} \right) \Rightarrow AH//CK\)

Xét tứ giác \(AHCK\) có:

\(\left\{ \begin{array}{l}
AH//CK\\
AH = CK
\end{array} \right.\left( \text{chứng minh trên} \right)\)

\( \Rightarrow \) tứ giác \(AHCK\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

Câu 2

Gọi \(O\) là trung điểm của \(HK\). Chứng minh rằng ba điểm \(A, O, C\) thẳng hàng

Phương pháp giải:

Áp dụng: Tính chất hình bình hành: Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Lời giải chi tiết:

Xét hình bình hành \(AHCK\) có \(O\) là trung điểm của \(HK\) (giả thiết)

\( \Rightarrow \) \(O\) là giao điểm của hai đường chéo \(AC\) và \(HK\) của hình bình hành (tính chất hình bình hành)

Hay \(A,O,C\) thẳng hàng.