Bài 18 trang 143 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Trên đường tròn (O ; R) vẽ dây cung AB sao cho số đo cung lớn AB gấp ba lần số đo cung nhỏ AB .
Đề bài
Trên đường tròn (O ; R) vẽ dây cung AB sao cho số đo cung lớn AB gấp ba lần số đo cung nhỏ AB .
a) Tính số đo và chiều dài các cung đó.
b) Tính các góc của tam giác OAB và khoảng cách từ O đến dây AB.
Phương pháp giải - Xem chi tiết
a) Tính số đo cung nhỏ AB và cung lớn AB, sử dụng công thức tính chiều dài cung n0 là \(l = \dfrac{{\pi Rn}}{{180}}\).
b) Chứng minh tam giác OAB vuông cân tại O, tính các góc của tam giác. Áp dụng định lí đường trung tuyến trong tam giác vuông tính khoảng cách từ O đến dây AB.
Lời giải chi tiết
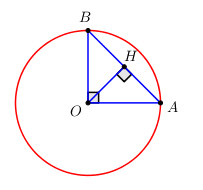
a) Ta có: Số đo cung lớn AB = 3 số đo cung nhỏ AB.
Mà Số đo cung lớn AB + số đo cung nhỏ AB = 3600
=>3 số đo cung nhỏ AB + số đo cung nhỏ AB = 3600
=> 4 số đo cung nhỏ AB = 3600
=> Số đo cung nhỏ AB\( = \dfrac{1}{4}{.360^0} = {90^0} \Rightarrow \) Số đo cung lớn AB \( = {3.90^0} = {270^0}\).
Chiều dài cung nhỏ AB là \(l = \dfrac{{\pi Rn}}{{180}} = \dfrac{{\pi .R.90}}{{180}} = \dfrac{{\pi R}}{2}\)
Chiều dài cung lớn AB là \(l' = \dfrac{{\pi Rn'}}{{180}} = \dfrac{{\pi R.270}}{{180}} = \dfrac{{3\pi R}}{2}\)
b) Ta có: \(\widehat {AOB} = sd\,cung\,AB = {90^0}\) (số đo góc ở tâm bằng số đo cung bị chắn) \( \Rightarrow \Delta OAB\) vuông tại O.
Lại có \(OA = OB = R \Rightarrow \Delta OAB\) vuông cân tại O \( \Rightarrow \widehat {OAB} = \widehat {OBA} = {45^0}\).
Gọi H là trung điểm của AB \( \Rightarrow OH \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).
\( \Rightarrow \) Khoảng cách từ O đến dây AB chính bằng OH.
Xét tam giác vuông OAB có : \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{R^2} + {R^2}}\)\(\, = \sqrt {2{R^2}} = R\sqrt 2 \)
\( \Rightarrow OH = \dfrac{1}{2}AB = \dfrac{{R\sqrt 2 }}{2}\) (định lí đường trung tuyến trong tam giác vuông).
Vậy khoảng cách từ O đến dây AB bằng \(\dfrac{{R\sqrt 2 }}{2}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 18 trang 143 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







