Bài 14 trang 142 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập CD là một đường kính của đường tròn (O), AB là một dây cung song song với CD. Vẽ dây cung AE song song
Đề bài
CD là một đường kính của đường tròn (O), AB là một dây cung song song với CD. Vẽ dây cung AE song song với CB, gọi F là giao điểm các đường thẳng AB và DE. Đường thẳng đi qua F song song với BC cắt đường thẳng CD tại G. Chứng minh GA tiếp xúc với đường tròn (O).
Phương pháp giải - Xem chi tiết
+) Gọi H là giao điểm của AC và GF.
+) Chứng minh tứ giác AFDG và CDFH là tứ giác nội tiếp.
+) Chứng minh tam giác GAC và tam giác GDA đồng dạng \( \Rightarrow \widehat {GAC} = \widehat {GDA}\).
Lời giải chi tiết
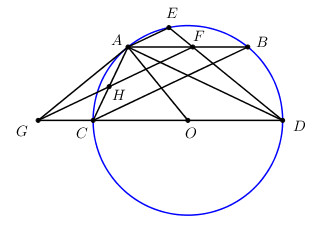
Vì BC // FG \( \Rightarrow \widehat {DCB} = \widehat {DGF}\) (hai góc đồng vị bằng nhau).
Mà \(\widehat {DCB} = \widehat {DAB}\) (hai góc nội tiếp cùng chắn cung BD) \( \Rightarrow \widehat {DGF} = \widehat {DAB}\) hay \(\widehat {DGF} = \widehat {DAF}\).
\( \Rightarrow \) Tứ giác AFDG là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn một cạnh dưới các góc bằng nhau) \( \Rightarrow \widehat {GAD} = \widehat {GFD}\) (1) (hai góc nội tiếp cùng chắn cung GD).
Gọi H là giao điểm của AC và GF.
Ta có: AE // FH \( \Rightarrow \widehat {AED} = \widehat {HFD}\) (hai góc đồng vị bằng nhau).
Mà \(\widehat {AED} + \widehat {ACD} = {180^0}\) (Tứ giác ACDE là tứ giác nội tiếp) \( \Rightarrow \widehat {HFD} + \widehat {ACD} = {180^0}\)
Lại có \(\widehat {ACD} + \widehat {ACG} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {HFD} = \widehat {ACG}\) hay \(\widehat {GFD} = \widehat {ACG}\) (2)
Từ (1) và (2) \( \Rightarrow \widehat {GAD} = \widehat {ACG}\).
Xét tam giác GAC và tam giác GDA có:
\(\widehat G\) chung;
\(\widehat {ACG} = \widehat {GAD}\,\,\left( {cmt} \right)\);
\( \Rightarrow \Delta GAC \sim \Delta GDA\,\,\left( {g.g} \right)\) \( \Rightarrow \widehat {GAC} = \widehat {GDA}\) (hai góc tương ứng).
Ta có: \(\widehat {GDA}\) là góc nội tiếp chắn cung AC).
\(\widehat {GAC}\) là góc ở vị trí tạo bởi tiếp tuyến và dây cung chắn cung AC.
Lại có \(\widehat {GAC} = \widehat {GDA}\,\,\left( {cmt} \right) \Rightarrow \) AG là tiếp tuyến của đường tròn \(\left( O \right)\) hay GA tiếp xúc với đường tròn (O) (đpcm).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 14 trang 142 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







