Bài 16 trang 170 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Cho tam giác MDN nhọn. Kẻ DE vuông góc với MN
Đề bài
Cho tam giác MDN nhọn. Kẻ DE vuông góc với MN \((E \in MN).\) Trên tia đối của tia ED lấy điểm F sao cho EF = ED. Chứng minh rằng :
a) \(\Delta DME = \Delta FME.\)
b) DN = FN.
Lời giải chi tiết
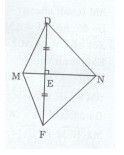
a)Xét tam giác DME và FME có:
DE = FE (gt)
\(\widehat {DEM} = \widehat {FEM}( = {90^0})\)
ME là cạnh chung.
Do đó: \(\Delta DME = \Delta FME(c.g.c)\)
b) Xét tam giác DEN và FEN ta có:
DE = FE (gt)
\(\widehat {DEN} = \widehat {FME}( = {90^0})\)
EN là cạnh chung.
Do đó: \(\Delta DEN = \Delta FEN(c.g.c) \Rightarrow DN = FN.\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 16 trang 170 Tài liệu dạy – học Toán 7 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 16 trang 170 Tài liệu dạy – học Toán 7 tập 1 timdapan.com"







