Bài 10 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao

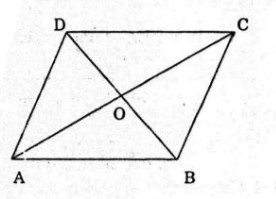
Cho hình bình hành \(ABCD\) với tâm \(O\). Hãy điền vào chỗ trống (…) để được đẳng thức đúng

LG a

\(\overrightarrow {AB}  + \overrightarrow {AD}  = ....\)  

Phương pháp giải:

Sử dụng quy tắc ba điểm, quy tắc hình bình hành:

Với ba điểm M, N, P bất kì ta có: \(\overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} \)

Nếu OABC là hình bình hành thì ta có:

\(\overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB} \)

Lời giải chi tiết:

\(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \) (quy tắc hình bình hành).

LG b

\(\overrightarrow {AB}  + \overrightarrow {CD}  = ......\)

Lời giải chi tiết:

\(\overrightarrow {AB}  + \overrightarrow {CD}  = \,\overrightarrow {AB}  + \overrightarrow {BA}   = \overrightarrow {AA} = \overrightarrow 0 \,\)

LG c

\(\overrightarrow {AB}  + \overrightarrow {OA}  = ......\)

Lời giải chi tiết:

\(\overrightarrow {AB}  + \overrightarrow {OA}  = \overrightarrow {OA}  + \overrightarrow {AB} \) (giao hoán)

\( = \overrightarrow {OB} \) (quy tắc ba điểm)

LG d

\(\overrightarrow {OA}  + \overrightarrow {OC}  = .......\)

Lời giải chi tiết:

\(\overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow 0 \) (vì O là trung điểm của AC).

LG e

\(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = ........\)

Lời giải chi tiết:

\(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD} \)

\(= (\overrightarrow {OA}  + \overrightarrow {OC} ) + (\overrightarrow {OB}  + \overrightarrow {OD} ) \) (giao hoán)

\(= \overrightarrow 0  + \overrightarrow 0  = \overrightarrow 0 \)

(vì O là trung điểm của AC).