Ôn tập chương 1 Phép dời hình và Phép đồng dạng trong mặt phẳng
.png)
1. Nội dung đã được học
a) Tổng quan
b) Các kí hiệu
c) Biểu thức tọa độ
d) Sơ đồ tính chất
2. Ghi nhớ phép biến hình qua sơ đồ tư duy
a) Sơ đồ các phép biến hình
.png)
b) Sơ đồ biểu diễn mối liên hệ giữa các phép biến hình
.png)
3. Bài tập ôn tập
Bài tập 1:
Trong mặt phẳng (Oxy) cho \(\overrightarrow u = \left( {1; - 2} \right)\)
a) Viết phương trình ảnh của mỗi đường trong trường hợp sau:
+) Đường thẳng a có phương trình: 3x - 5y + 1 = 0 ?
+) Đường thẳng b có phương trình: 2x + y + 100 = 0
b) Viết phương trình đường tròn ảnh của đường tròn (C ): \({x^2} + {y^2} - 4{\rm{x}} + y - 1 = 0\)
c) Viết phương trình đường (E) ảnh của (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\)
d) Viết phương trình ảnh của (H): \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Lời giải:
a) Gọi M(x;y) thuộc các đường đã cho và M’(x’;y’) thuộc các đường ảnh của chúng.
Theo công thức tọa độ của phép tịnh tiến ta có: \(\left\{ \begin{array}{l}x' = 1 + x\\y' = - 2 + y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = x' - 1\\y = y' + 2\end{array} \right.\)
Thay x, y vào phương trình các đường ta có:
Đường thẳng a’: 3(x’-1) - 5(y’+2) + 1 = 0 ⇔ 3x’ - 5y’ - 12 = 0
Đường thẳng b’: 2(x’ - 1) + (y’+2) + 100 = 0 hay 2x’ + y’ + 100 = 0
b) Đường tròn (C’):
\({\left( {x' - 1} \right)^2} + {\left( {y' + 2} \right)^2} - 4\left( {x' - 1} \right) + \)
\(\,\,\,y' + 2 - 1 = 0\)
Hay \({x^2} + {y^2} - 6{\rm{x}} + 5y + 10 = 0\)
c) Đường (E’): \(\frac{{{{\left( {x' - 1} \right)}^2}}}{9} + \frac{{{{\left( {y' + 2} \right)}^2}}}{4} = 1\)
\(\Leftrightarrow \frac{{{{\left( {x - 1} \right)}^2}}}{9} + \frac{{{{\left( {y + 2} \right)}^2}}}{4} = 1\)
d) Đường (H’): \(\frac{{{{\left( {x' - 1} \right)}^2}}}{{16}} - \frac{{{{\left( {y' + 2} \right)}^2}}}{9} = 1 \)
\(\Leftrightarrow \frac{{{{\left( {x - 1} \right)}^2}}}{{16}} - \frac{{{{\left( {y + 2} \right)}^2}}}{9} = 1\).
Bài tập 2:
Cho điểm M(2;-3). Tìm ảnh của điểm M qua phép đối xứng trục d: y-2x=0.
Lời giải:
Gọi N(x;y) là điểm đối xứng với M qua d và H là trung điểm của MN thì M,N đối xứng nhau qua d thì điều kiện là: \(\left\{ \begin{array}{l}\overrightarrow {MN} .\overrightarrow U = 0\quad \left( 1 \right)\\H \in d\quad \quad \left( 2 \right)\end{array} \right.\,\)
Ta có:
\(\begin{array}{l}
\overrightarrow {MN} = \left( {x - 2;y + 3} \right)\\
\vec U = \left( {1;2} \right)\\
H = \left( {\frac{{x + 2}}{2};\frac{{y - 3}}{2}} \right)
\end{array}\)
Điều kiện (*) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\left( {x - 2} \right).1 + \left( {y + 3} \right).2 = 0}\\
{\frac{{x + 2}}{2} = \frac{{y - 3}}{2}}
\end{array}} \right.\)
\(\begin{array}{l}
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x + 2y + 4 = 0}\\
{y = x + 5}
\end{array}} \right.\\
\Rightarrow \left\{ {\begin{array}{*{20}{l}}
{y = \frac{1}{3}}\\
{x = - \frac{{14}}{3}}
\end{array}} \right. \Rightarrow N = \left( { - \frac{{14}}{3};\frac{1}{3}} \right).
\end{array}\)
Bài tập 3:
Trong mặt phẳng Oxy cho đường tròn (O;R) : \({x^2} + {y^2} + 2{\rm{x}} - 6y + 6 = 0\)và (E) : \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) điểm I(1;2). Tìm ảnh của (O;R) và (E) qua phép đối xứng tâm I.
Lời giải:
Gọi M(x;y) là điểm bất kỳ thuộc (O;R) và (E).
M’(x’;y’) là ảnh của M qua phép đối xứng tâm I.
Khi đó I là trung điểm của MM’ nên ta có:
\(\left\{ \begin{array}{l}{x_I} = \frac{{x + x'}}{2}\\{y_I} = \frac{{y + y'}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 2.1 - x\\y' = 2.2 - y\end{array} \right.\)
\(\begin{array}{l}
\Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 2 - x'}\\
{y = 4 - y'}
\end{array}} \right.\\
\Rightarrow \left[ {\begin{array}{*{20}{l}}
\begin{array}{l}
{\left( {2 - x'} \right)^2} + {\left( {4 - y'} \right)^2} + 2\left( {2 - x'} \right)\\
\,\,\,\,\,\,\,\,\, - 6\left( {4 - y'} \right) + 6 = 0
\end{array}\\
{\frac{{{{\left( {2 - x'} \right)}^2}}}{9} + \frac{{{{\left( {4 - y'} \right)}^2}}}{4} = 1}
\end{array}} \right.
\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + {y^2} - 6{\rm{x}} - 2y + 6 = 0\\\frac{{{{\left( {2 - x} \right)}^2}}}{9} + \frac{{{{\left( {4 - y} \right)}^2}}}{4} = 1\end{array} \right.\)
Vậy ảnh của (O;R) và (E) qua phép đối xứng tâm I có phương trình lần lượt là:
\({x^2} + {y^2} - 6{\rm{x}} - 2y + 6 = 0;\)
\(\frac{{{{\left( {2 - x} \right)}^2}}}{9} + \frac{{{{\left( {4 - y} \right)}^2}}}{4} = 1\).
Bài tập 4:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (O): \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4.\) Tìm phương trình đường tròn (O’) là ảnh của (O) qua phép vị tự tâm O tỉ số k = 2.
Lời giải:
Tâm I của (O) có tọa độ I(1;1) bán kính R = 2.
Nếu (O’) có tâm là J và bán kính R’ là ảnh của (O) qua phép vị tự tâm O ta có đẳng thức vectơ:
\(\overrightarrow {{\rm{OJ}}} = 2\overrightarrow {OI} \Leftrightarrow \left\{ \begin{array}{l}x' - 0 = 2.1\\y' - 0 = 2.1\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}x' = 2\\y' = 2\end{array} \right. \Rightarrow J\left( {2;2} \right)\).
\(R' = 2R = 2.2 = 4\).
Vậy (O’): \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 16\).
.png)
1. Nội dung đã được học
a) Tổng quan
b) Các kí hiệu
c) Biểu thức tọa độ
d) Sơ đồ tính chất
2. Ghi nhớ phép biến hình qua sơ đồ tư duy
a) Sơ đồ các phép biến hình
.png)
b) Sơ đồ biểu diễn mối liên hệ giữa các phép biến hình
.png)
3. Bài tập ôn tập
Bài tập 1:
Trong mặt phẳng (Oxy) cho \(\overrightarrow u = \left( {1; - 2} \right)\)
a) Viết phương trình ảnh của mỗi đường trong trường hợp sau:
+) Đường thẳng a có phương trình: 3x - 5y + 1 = 0 ?
+) Đường thẳng b có phương trình: 2x + y + 100 = 0
b) Viết phương trình đường tròn ảnh của đường tròn (C ): \({x^2} + {y^2} - 4{\rm{x}} + y - 1 = 0\)
c) Viết phương trình đường (E) ảnh của (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\)
d) Viết phương trình ảnh của (H): \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Lời giải:
a) Gọi M(x;y) thuộc các đường đã cho và M’(x’;y’) thuộc các đường ảnh của chúng.
Theo công thức tọa độ của phép tịnh tiến ta có: \(\left\{ \begin{array}{l}x' = 1 + x\\y' = - 2 + y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = x' - 1\\y = y' + 2\end{array} \right.\)
Thay x, y vào phương trình các đường ta có:
Đường thẳng a’: 3(x’-1) - 5(y’+2) + 1 = 0 ⇔ 3x’ - 5y’ - 12 = 0
Đường thẳng b’: 2(x’ - 1) + (y’+2) + 100 = 0 hay 2x’ + y’ + 100 = 0
b) Đường tròn (C’):
\({\left( {x' - 1} \right)^2} + {\left( {y' + 2} \right)^2} - 4\left( {x' - 1} \right) + \)
\(\,\,\,y' + 2 - 1 = 0\)
Hay \({x^2} + {y^2} - 6{\rm{x}} + 5y + 10 = 0\)
c) Đường (E’): \(\frac{{{{\left( {x' - 1} \right)}^2}}}{9} + \frac{{{{\left( {y' + 2} \right)}^2}}}{4} = 1\)
\(\Leftrightarrow \frac{{{{\left( {x - 1} \right)}^2}}}{9} + \frac{{{{\left( {y + 2} \right)}^2}}}{4} = 1\)
d) Đường (H’): \(\frac{{{{\left( {x' - 1} \right)}^2}}}{{16}} - \frac{{{{\left( {y' + 2} \right)}^2}}}{9} = 1 \)
\(\Leftrightarrow \frac{{{{\left( {x - 1} \right)}^2}}}{{16}} - \frac{{{{\left( {y + 2} \right)}^2}}}{9} = 1\).
Bài tập 2:
Cho điểm M(2;-3). Tìm ảnh của điểm M qua phép đối xứng trục d: y-2x=0.
Lời giải:
Gọi N(x;y) là điểm đối xứng với M qua d và H là trung điểm của MN thì M,N đối xứng nhau qua d thì điều kiện là: \(\left\{ \begin{array}{l}\overrightarrow {MN} .\overrightarrow U = 0\quad \left( 1 \right)\\H \in d\quad \quad \left( 2 \right)\end{array} \right.\,\)
Ta có:
\(\begin{array}{l}
\overrightarrow {MN} = \left( {x - 2;y + 3} \right)\\
\vec U = \left( {1;2} \right)\\
H = \left( {\frac{{x + 2}}{2};\frac{{y - 3}}{2}} \right)
\end{array}\)
Điều kiện (*) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\left( {x - 2} \right).1 + \left( {y + 3} \right).2 = 0}\\
{\frac{{x + 2}}{2} = \frac{{y - 3}}{2}}
\end{array}} \right.\)
\(\begin{array}{l}
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x + 2y + 4 = 0}\\
{y = x + 5}
\end{array}} \right.\\
\Rightarrow \left\{ {\begin{array}{*{20}{l}}
{y = \frac{1}{3}}\\
{x = - \frac{{14}}{3}}
\end{array}} \right. \Rightarrow N = \left( { - \frac{{14}}{3};\frac{1}{3}} \right).
\end{array}\)
Bài tập 3:
Trong mặt phẳng Oxy cho đường tròn (O;R) : \({x^2} + {y^2} + 2{\rm{x}} - 6y + 6 = 0\)và (E) : \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) điểm I(1;2). Tìm ảnh của (O;R) và (E) qua phép đối xứng tâm I.
Lời giải:
Gọi M(x;y) là điểm bất kỳ thuộc (O;R) và (E).
M’(x’;y’) là ảnh của M qua phép đối xứng tâm I.
Khi đó I là trung điểm của MM’ nên ta có:
\(\left\{ \begin{array}{l}{x_I} = \frac{{x + x'}}{2}\\{y_I} = \frac{{y + y'}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 2.1 - x\\y' = 2.2 - y\end{array} \right.\)
\(\begin{array}{l}
\Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 2 - x'}\\
{y = 4 - y'}
\end{array}} \right.\\
\Rightarrow \left[ {\begin{array}{*{20}{l}}
\begin{array}{l}
{\left( {2 - x'} \right)^2} + {\left( {4 - y'} \right)^2} + 2\left( {2 - x'} \right)\\
\,\,\,\,\,\,\,\,\, - 6\left( {4 - y'} \right) + 6 = 0
\end{array}\\
{\frac{{{{\left( {2 - x'} \right)}^2}}}{9} + \frac{{{{\left( {4 - y'} \right)}^2}}}{4} = 1}
\end{array}} \right.
\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + {y^2} - 6{\rm{x}} - 2y + 6 = 0\\\frac{{{{\left( {2 - x} \right)}^2}}}{9} + \frac{{{{\left( {4 - y} \right)}^2}}}{4} = 1\end{array} \right.\)
Vậy ảnh của (O;R) và (E) qua phép đối xứng tâm I có phương trình lần lượt là:
\({x^2} + {y^2} - 6{\rm{x}} - 2y + 6 = 0;\)
\(\frac{{{{\left( {2 - x} \right)}^2}}}{9} + \frac{{{{\left( {4 - y} \right)}^2}}}{4} = 1\).
Bài tập 4:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (O): \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4.\) Tìm phương trình đường tròn (O’) là ảnh của (O) qua phép vị tự tâm O tỉ số k = 2.
Lời giải:
Tâm I của (O) có tọa độ I(1;1) bán kính R = 2.
Nếu (O’) có tâm là J và bán kính R’ là ảnh của (O) qua phép vị tự tâm O ta có đẳng thức vectơ:
\(\overrightarrow {{\rm{OJ}}} = 2\overrightarrow {OI} \Leftrightarrow \left\{ \begin{array}{l}x' - 0 = 2.1\\y' - 0 = 2.1\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}x' = 2\\y' = 2\end{array} \right. \Rightarrow J\left( {2;2} \right)\).
\(R' = 2R = 2.2 = 4\).
Vậy (O’): \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 16\).
.PNG)
.PNG)
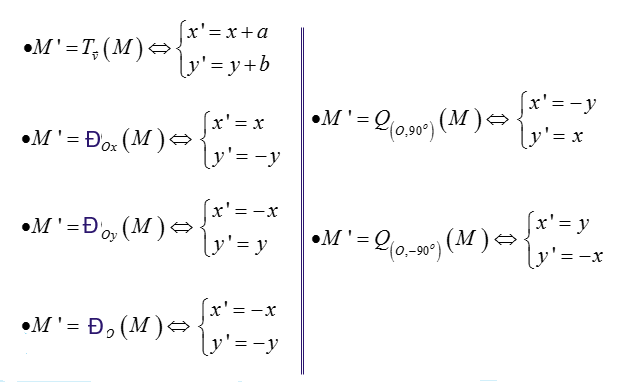
.PNG)