Bài 8: Phép đồng dạng
1. Định nghĩa phép đồng dạng
Phép biến hình F gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm M, N bất kì và ảnh M’, N’ của chúng ta có:
\(M'N' = k.{\rm{MN}}\)
\(\left\{ \begin{array}{l}F(M) = M'\\F(N) = N'\end{array} \right. \Rightarrow M'N' = k.MN\,\,(k > 0)\)
Nhận xét:
+ Phép dời hình là phép đồng dạng tỉ số k = 1.
+ Phép vị tự \({V_{\left( {I,k} \right)}}\) là phép đồng dạng tỉ số \(\left| k \right|.\)
+ Mối quan hệ giữa phép dời hình, phép vị tự, phép đồng dạng có thể biểu diễn bằng sơ đồ sau:
Chú ý:
Cho phép vị tự \({V_{\left( {I;k} \right)}}\)
Phép dời hình D
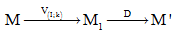
Ta nó rằng F là phép hợp thành của hai phép biến hình V và D.
Hoặc có thể nói F là tích của hai phép biến hình V và D.
Kí hiệu F = D.V.
Vậy để xác định ảnh của một điểm M qua phép biến hình tích F = D.V ta làm như sau:
- Xác định ảnh của M qua phép vị tự V được ảnh \({M_1}.\)
- Xác định ảnh của \({M_1}\) qua phép dời hình D ta được M’.
Ta được M’ là ảnh của M qua phép biến hình F=D.V.
2. Định lý
Mọi phép đồng dạng F tỉ số k đều là hợp thành của một phép vị tự V tỉ số k và một phép dời hình D.
3. Tính chất của phép đồng dạng
Từ định lý trên, ta có các hệ quả sau:
Phép đồng dạng tỉ số k:
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
- Biến đường thẳng thành đường thẳng.
- Biến tia thành tia.
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k (k là tỉ số phép đồng dạng).
- Biến tam giác thành tam giác đồng dạng tỉ số k.
- Biến đường tròn có bán kính R thành đường tròn có bán kính kR.
- Biến góc thành góc bằng nó.
Nhận xét:
Ta thấy phép vị tự có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.
Trong trường hợp tổng quát phép dời hình không có tính chất đó.
Ví dụ: Phép quay với một góc quay khác \(k\pi .\)
Mà phép đồng dạng là hợp thành của phép vị tự và phép dời hình nên cũng không có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.
4. Hai hình đồng dạng
.jpg)
Có phép vị tự V biến hình H thành hình \({H_{1,}}\) có phép biến hình D biến hình \({H_1}\) thành hình H’.
Nếu gọi F là phép hợp thành của V và D thì F là phép đồng dạng biến H thành H’.
Ta nói rằng hai hình H và H’ đồng dạng với nhau.
Định nghĩa
Hai hình gọi là đồng dạng nếu có phép đồng dạng biến hình này thành hình kia.
So sánh phép dời hình, vị tự V(O,k), đồng dạng tỉ số k
- Giống nhau:
+ Biến ba điểm thẳng hàng thành ba điểm thẳng hàng (và không làm thay đổi thứ tự của ba điểm đó).
+ Biến đường thẳng thành đường thẳng, tia thành tia, biến góc thành góc bằng nó.
- Sự khác nhau:
+ Phép dời hình
- Biến đoạn thẳng thành đoạn thẳng bằng nó.
- Biến tam giác thành tam giác bằng tam giác đó.
- Biến đường tròn thành đường tròn có bán kính bằng đường tròn đã cho.
+ Phép vị tự
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với |k|.
- Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là |k|.
- Biến đường tròn thành đường tròn có bán kính có bán kính là |k|R.
+ Phép đồng dạng
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k.
- Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là k.
- Biến đường tròn thành đường tròn có bán kính có bán kính là kR.
5. Bài tập minh họa
Ví dụ 1:
Cho đường thẳng \(d:x - y + 1 = 0,\) viết phương trình d’ là ảnh của đường thẳng d qua phép đồng dạng bằng cách thực hiện qua phép vị tự tâm I(1;1), tỉ số k=2 và phép tịnh tiến theo vectơ \(\overrightarrow v = ( - 2; - 1).\)
Lời giải:
Ta có \(M(0;1) \in d\)
Qua phép vị tự tâm I, tỉ số k=2 ta có: \({V_{\left( {I;2} \right)}}(d) = {d_1}.\)
Suy ra phương trình \({d_1}\) có dạng: \(x - y + c = 0.\)
Mặt khác: \({V_{\left( {I;2} \right)}}(M) = {M_1}({x_1};{y_1}) \in {d_1}\)
\( \Rightarrow \overrightarrow {{{{\mathop{\rm IM}\nolimits} }_1}} = 2.\overrightarrow {IM} \Rightarrow {M_1}\left( { - 1;1} \right).\)
Vậy \({d_1}:x - y + 2 = 0.\)
Qua phép tịnh tiến theo vectơ \(\overrightarrow v ,\)ta có: \({T_{\overrightarrow V }}({d_1}) = {d_2}\)
Suy ra phương trình \({d_2}\) có dạng: \(x - y + d = 0.\)
Mặt khác: \({M_1} \in {d_1} \Rightarrow {T_{\overrightarrow v }}({M_1}) = {M_2}({x_2};{y_2}) \in {d_2}\)
\( \Rightarrow \overrightarrow {{M_1}{M_2}} = \overrightarrow v \Rightarrow {M_2}( - 2;1).\)
Vậy \({d_2}\) có phương trình: \(x - y + 3 = 0.\)
Qua phép đồng dạng đường thẳng \(d:x - y + 1 = 0\) trở thành đường thẳng \({d_2}:x - y + 3 = 0.\)
Ví dụ 2:
Cho đường tròn \(\left( C \right):{(x - 1)^2} + {(y - 2)^2} = 4.\) Xác định ảnh của (C) qua phép vị tự tâm O, tỉ số k = -2 và phép đối xứng trục Oy.
Lời giải:
(C) có tâm I(1;2) bán kính R = 2.
Gọi I’ và R’ lần lượt là tâm và bán kính của (C’) là ảnh của (C) qua phép vị tự tâm O, tỉ số k = -2.
Suy ra: R’ = 4.
Ta có: \({V_{\left( {O; - 2} \right)}}(I) = I' \Rightarrow \overrightarrow {OI'} = - 2\overrightarrow {OI} \)
\(\Rightarrow I'( - 2; - 4)\)
Vậy phương trình của (C’) là: \({(x + 2)^2} + {(y + 4)^2} = 16.\)
Gọi I’’, R’’ lần lượt là tâm và bán kính của đường tròn (C’’) là ảnh của (C’) qua phép đối xứng trục Oy.
Suy ra: \(R'' = 4.\)
I’’ = ĐOy(I’)\( \Rightarrow \left\{ \begin{array}{l}{x_{I''}} = - {x_{I'}} = 2\\{y_{I''}} = {y_{I'}} = - 4\end{array} \right.\)
Vậy phương trình (C’’) là: \({(x - 2)^2} + {(y + 4)^2} = 16.\)
1. Định nghĩa phép đồng dạng
Phép biến hình F gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm M, N bất kì và ảnh M’, N’ của chúng ta có:
\(M'N' = k.{\rm{MN}}\)
\(\left\{ \begin{array}{l}F(M) = M'\\F(N) = N'\end{array} \right. \Rightarrow M'N' = k.MN\,\,(k > 0)\)
Nhận xét:
+ Phép dời hình là phép đồng dạng tỉ số k = 1.
+ Phép vị tự \({V_{\left( {I,k} \right)}}\) là phép đồng dạng tỉ số \(\left| k \right|.\)
+ Mối quan hệ giữa phép dời hình, phép vị tự, phép đồng dạng có thể biểu diễn bằng sơ đồ sau:
Chú ý:
Cho phép vị tự \({V_{\left( {I;k} \right)}}\)
Phép dời hình D
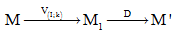
Ta nó rằng F là phép hợp thành của hai phép biến hình V và D.
Hoặc có thể nói F là tích của hai phép biến hình V và D.
Kí hiệu F = D.V.
Vậy để xác định ảnh của một điểm M qua phép biến hình tích F = D.V ta làm như sau:
- Xác định ảnh của M qua phép vị tự V được ảnh \({M_1}.\)
- Xác định ảnh của \({M_1}\) qua phép dời hình D ta được M’.
Ta được M’ là ảnh của M qua phép biến hình F=D.V.
2. Định lý
Mọi phép đồng dạng F tỉ số k đều là hợp thành của một phép vị tự V tỉ số k và một phép dời hình D.
3. Tính chất của phép đồng dạng
Từ định lý trên, ta có các hệ quả sau:
Phép đồng dạng tỉ số k:
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
- Biến đường thẳng thành đường thẳng.
- Biến tia thành tia.
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k (k là tỉ số phép đồng dạng).
- Biến tam giác thành tam giác đồng dạng tỉ số k.
- Biến đường tròn có bán kính R thành đường tròn có bán kính kR.
- Biến góc thành góc bằng nó.
Nhận xét:
Ta thấy phép vị tự có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.
Trong trường hợp tổng quát phép dời hình không có tính chất đó.
Ví dụ: Phép quay với một góc quay khác \(k\pi .\)
Mà phép đồng dạng là hợp thành của phép vị tự và phép dời hình nên cũng không có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.
4. Hai hình đồng dạng
.jpg)
Có phép vị tự V biến hình H thành hình \({H_{1,}}\) có phép biến hình D biến hình \({H_1}\) thành hình H’.
Nếu gọi F là phép hợp thành của V và D thì F là phép đồng dạng biến H thành H’.
Ta nói rằng hai hình H và H’ đồng dạng với nhau.
Định nghĩa
Hai hình gọi là đồng dạng nếu có phép đồng dạng biến hình này thành hình kia.
So sánh phép dời hình, vị tự V(O,k), đồng dạng tỉ số k
- Giống nhau:
+ Biến ba điểm thẳng hàng thành ba điểm thẳng hàng (và không làm thay đổi thứ tự của ba điểm đó).
+ Biến đường thẳng thành đường thẳng, tia thành tia, biến góc thành góc bằng nó.
- Sự khác nhau:
+ Phép dời hình
- Biến đoạn thẳng thành đoạn thẳng bằng nó.
- Biến tam giác thành tam giác bằng tam giác đó.
- Biến đường tròn thành đường tròn có bán kính bằng đường tròn đã cho.
+ Phép vị tự
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với |k|.
- Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là |k|.
- Biến đường tròn thành đường tròn có bán kính có bán kính là |k|R.
+ Phép đồng dạng
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k.
- Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là k.
- Biến đường tròn thành đường tròn có bán kính có bán kính là kR.
5. Bài tập minh họa
Ví dụ 1:
Cho đường thẳng \(d:x - y + 1 = 0,\) viết phương trình d’ là ảnh của đường thẳng d qua phép đồng dạng bằng cách thực hiện qua phép vị tự tâm I(1;1), tỉ số k=2 và phép tịnh tiến theo vectơ \(\overrightarrow v = ( - 2; - 1).\)
Lời giải:
Ta có \(M(0;1) \in d\)
Qua phép vị tự tâm I, tỉ số k=2 ta có: \({V_{\left( {I;2} \right)}}(d) = {d_1}.\)
Suy ra phương trình \({d_1}\) có dạng: \(x - y + c = 0.\)
Mặt khác: \({V_{\left( {I;2} \right)}}(M) = {M_1}({x_1};{y_1}) \in {d_1}\)
\( \Rightarrow \overrightarrow {{{{\mathop{\rm IM}\nolimits} }_1}} = 2.\overrightarrow {IM} \Rightarrow {M_1}\left( { - 1;1} \right).\)
Vậy \({d_1}:x - y + 2 = 0.\)
Qua phép tịnh tiến theo vectơ \(\overrightarrow v ,\)ta có: \({T_{\overrightarrow V }}({d_1}) = {d_2}\)
Suy ra phương trình \({d_2}\) có dạng: \(x - y + d = 0.\)
Mặt khác: \({M_1} \in {d_1} \Rightarrow {T_{\overrightarrow v }}({M_1}) = {M_2}({x_2};{y_2}) \in {d_2}\)
\( \Rightarrow \overrightarrow {{M_1}{M_2}} = \overrightarrow v \Rightarrow {M_2}( - 2;1).\)
Vậy \({d_2}\) có phương trình: \(x - y + 3 = 0.\)
Qua phép đồng dạng đường thẳng \(d:x - y + 1 = 0\) trở thành đường thẳng \({d_2}:x - y + 3 = 0.\)
Ví dụ 2:
Cho đường tròn \(\left( C \right):{(x - 1)^2} + {(y - 2)^2} = 4.\) Xác định ảnh của (C) qua phép vị tự tâm O, tỉ số k = -2 và phép đối xứng trục Oy.
Lời giải:
(C) có tâm I(1;2) bán kính R = 2.
Gọi I’ và R’ lần lượt là tâm và bán kính của (C’) là ảnh của (C) qua phép vị tự tâm O, tỉ số k = -2.
Suy ra: R’ = 4.
Ta có: \({V_{\left( {O; - 2} \right)}}(I) = I' \Rightarrow \overrightarrow {OI'} = - 2\overrightarrow {OI} \)
\(\Rightarrow I'( - 2; - 4)\)
Vậy phương trình của (C’) là: \({(x + 2)^2} + {(y + 4)^2} = 16.\)
Gọi I’’, R’’ lần lượt là tâm và bán kính của đường tròn (C’’) là ảnh của (C’) qua phép đối xứng trục Oy.
Suy ra: \(R'' = 4.\)
I’’ = ĐOy(I’)\( \Rightarrow \left\{ \begin{array}{l}{x_{I''}} = - {x_{I'}} = 2\\{y_{I''}} = {y_{I'}} = - 4\end{array} \right.\)
Vậy phương trình (C’’) là: \({(x - 2)^2} + {(y + 4)^2} = 16.\)
.PNG)