Đề thi tháng môn Toán lớp 10 có đáp án

Đề thi tháng môn Toán lớp 10 trường THPT Ngô Sĩ Liên, Bắc Giang năm 2015 - 2016 (Lần 2) gồm 6 câu hỏi làm trong thời gian 120 phút, có đáp án đi kèm. Đây là tài liệu ôn tập môn Toán hữu ích dành cho các bạn học sinh lớp 10, mời các bạn tham khảo.

Bảng công thức lượng giác dùng cho lớp 10 - 11 - 12

Đề thi khảo sát chất lượng lần 2 môn Toán lớp 10 trường THPT Thạch Thành 1, Thanh Hóa năm 2015 - 2016

Đề thi học kì 2 môn Toán lớp 10 trường THPT Phan Ngọc Hiển, Cà Mau năm 2014 - 2015

Câu 1. (2,0 điểm): Cho hàm số y = x² - 4x + 3 (1)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
b) Biện luận theo m số nghiệm của phương trình x² - 4x + 3 = m.

Câu 2. (2,0 điểm): Giải các phương trình sau:

a) |x - 1| = 2x2 - 4x - 1

b)

Câu 3. (2,0 điểm): Cho tam giác ABC có trọng tâm G, N là điểm bất kì.

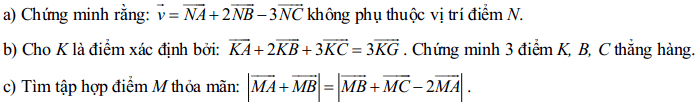
Câu 4. (2,0 điểm): Trong mặt phẳng toạ độ Oxy cho ba điểm A(-1;1), B(3;1), C(6;0).

a) Chứng minh rằng ba điểm A, B, C là ba đỉnh của một tam giác. Tìm toạ độ điểm D đối xứng với C qua A.

b) Gọi M là điểm trên cạnh BC sao cho: BC = 4MC. Chứng minh rằng:

Câu 5. (1,0 điểm): Giải hệ phương trình sau:

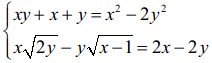
Câu 6. (1,0 điểm): Cho x, y là các số thực dương thỏa mãn x + y ≥ 3. Chứng minh rằng:

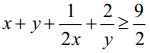
Đáp án đề thi tháng môn Toán lớp 10

Câu 1. Cho hàm số y = x² - 4x + 3 (1)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).

• Tìm TXĐ, lập BBT đúng 0.5
• Nêu đúng dạng đồ thị, toạ độ đỉnh, trục đối xứng, giao với trục toạ độ... 0.25
• Vẽ đồ thị đúng, đẹp 0.25

b) Biện luận theo m số nghiệm của phương trình x² - 4x + 3 = m (1)

Số nghiệm của phương trình (1) là số giao điểm của ĐTHS x² - 4x + 3 = m

và đường thẳng (d): y = m ((d) // Ox hoặc (d) trùng Ox)

Dựa vào đồ thị (P) ta có:

Với < -1 → (d) ∩ (P) = ∅ → phương trình vô nghiệm

Với m < -1 → (d) tiếp xúc với (P) tại 1 điểm I (2;-1) → (1) có 1 nghiệm x = 2

Với m > -1 → (d) cắt (P) tại 2 điểm phân biệt → (1) có 2 nghiệm phân biệt.

Câu 2.1 Giải các phương trình sau:

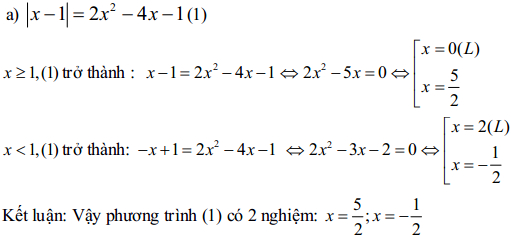
Câu 2.2

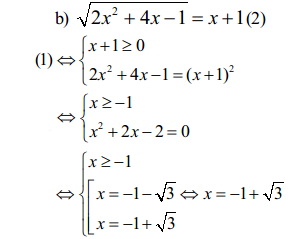
Vậy phương trình có nghiệm x = -1 + √3

(Còn tiếp)