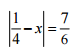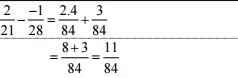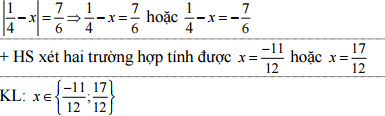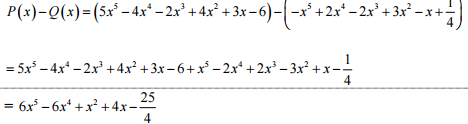Đề thi học kì 2 môn Toán lớp 7 có đáp án

Đề thi học kì 2 môn Toán lớp 7 sở GD&ĐT Bắc Giang năm 2015 - 2016 là tài liệu luyện thi học kỳ 2 lớp 7 rất hiệu quả. Đây cũng là tài liệu tham khảo môn Toán giúp các bạn học sinh lớp 7 ôn tập lại kiến thức, nhằm học tập môn Toán lớp 7 tốt hơn, đạt điểm cao trong bài thi giữa kì, thi cuối kì. Mời các bạn tham khảo.

Đề thi học kì 2 môn Địa lý lớp 7 trường THCS Bình Giang, Hòn Đất năm 2015 - 2016

Đề thi học kì 2 môn Sinh học lớp 7 phòng GD&ĐT Cam Lộ, Quảng Trị năm 2015 - 2016

Câu 1. (2,0 điểm)

a) Thực hiện phép tính:

b) Tính giá trị của biểu thức 3x² -2xy + 6 tại x = -1 và y =2

Câu 2. (3,0 điểm)

a) Tìm x ∈ R, biết:

b) Hãy thu gọn đơn thức, sau đó chỉ ra hệ số, phần biến và bậc của đơn thức.

c) Tìm nghiệm của đa thức 3 - 2x

Câu 3. (1,5 điểm) Cho hai đa thức:

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến.

b) Tìm đa thức A(x) = P(x) - Q(x).

Câu 4. (3,0 điểm)

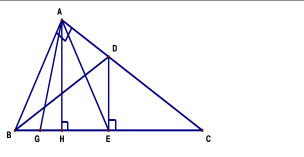
Cho tam giác ABC vuông tại A, biết và AB = 6cm. Trên cạnh BC lấy điểm E sao cho BA = BE. Đường thẳng vuông góc với BC tại E cắt AC tại D.

a) Chứng minh ΔABD = ΔEBD.

b) Chứng minh ΔABE là tam giác đều và tính độ dài cạnh BC.

c) Vẽ AH vuông góc với BC tại H. Tia phân giác của cắt BC tại G. Chứng minh rằng CA= CG.

Câu 5. (0,5 điểm)

Cho ba đa thức: A = 3x - 3y² - 2z; B = 2x - x² - 4y; C = 4y - 5z² - 3x với x, y, z là các số khác 0. Chứng minh rằng trong ba đa thức trên có ít nhất một đa thức có giá trị âm.

Đáp án đề thi học kì 2 môn Toán lớp 7

Đề thi học kì 2 môn Vật lý lớp 7 phòng GD&ĐT Bảo Lộc, Lâm Đồng năm 2014 - 2015

Đề thi học kì 2 môn Toán lớp 7 trường THCS Cửa Nam, Nghệ An năm 2015 - 2016

Câu 1:

a)

b) Thay x = -1, y = 2 vào biểu thức ta được:

3x² - 2xy + 6 = 3(-1)² - 2.(-1).2

= 3 + 2.2 = 7

Câu 2:

a)

b) A = -3/4x⁵y² (-8x³y) = 6x⁸y³

Đơn thức A có: Hệ số là 6

Phần biến là x⁸y³

Bậc là 11

c) 3 - 2x = 0

<=> 2x = 3 <=> x = 3/2

Câu 3:

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến

P(x) = 5x⁵ - 4x⁴ - 2x³ + 4x² + 3x - 6

Q(x) = -x⁵ + 2x⁴ - 2x³ + 3x² - x + 1/4

b)

Câu 4:

Câu 5:

Ta có: A = 3x - 2y² - 2z; B = 2z - x² - 4y; C = 4y - 5z² - 3x

Nên A + B + C = 3x - 2y² - 2z + 2z - x² - 4y + 4y - 5z² - 3x

= -x² - 2y² - 5z²

Chỉ ra với x, y, x ≠ 0 thì -x² - 2y² - 5z² <0

=> A + B + C < 0 => Trong ba đa thức A, B, C có ít nhất một đa thức có giá trị âm (ĐPCM)