Đề thi giữa học kì 2 môn Toán lớp 10 có đáp án

Đề thi giữa học kì 2 môn Toán lớp 10 trường THPT Thủ Đức, TP. HCM năm 2015 - 2016 có 4 câu hỏi và đáp án đi kèm, là tài liệu ôn tập môn Toán, chuẩn bị cho bài thi cuối năm hữu ích dành cho các bạn học sinh lớp 10. Mời các bạn tham khảo.

Đề thi giữa học kì 2 môn Toán lớp 10 trường THPT Hiệp Bình, Hồ Chí Minh năm 2014 - 2015

Đề thi học kì 2 môn Toán lớp 10 trường THPT Đa Phúc, Hà Nội năm 2015

Đề thi học kì 2 môn Toán lớp 10 trường THPT Gia Định, TP. Hồ Chí Minh

Câu 1. (4 điểm) Giải các bất phương trình sau:

Câu 2. (1 điểm) Định m để bất phương trình sau luôn nghiệm đúng với mọi x thuộc R:

x² + 2(m + 1)x + 9m - 5 > 0

Câu 3. (1 điểm) Một xí nghiệp sản xuất 2 loại sản phẩm I và II. Để sản xuất ra 1 sản phẩm I cần 2kg nguyên liệu loại A và 1kg nguyên liệu loại B. Để sản xuất ra 1 sản phẩm II cần 1kg nguyên liệu loại A và 2kg nguyên liệu loại B. Lượng nguyên liệu dự trữ loại A và B hiện có lần lượt là 30kg và 24kg. Biết lợi nhuận bán ra của 1 sản phẩm loại I là 8 triệu đồng và 1 sản phẩm loại II là 6 triệu đồng. Hãy tìm phương án sản xuất đạt lợi nhuận cao nhất.

Câu 4. (4 điểm) Cho ABC biết: A(4;5), B(1;1) và I(0;–2) là tâm đường tròn nội tiếp ABC.

a) Viết phương trình đường thẳng AB.

b) Tính cosin của góc tạo bởi hai đường thảng AB và AI.

c) Tính khoảng cách từ I đến đường thẳng AB. Viết phương trình đường thẳng BC.

Đáp án đề thi giữa học kì 2 môn Toán lớp 10

Câu 1. (5 điểm) Giải các bất phương trình sau:

a) (x + 2)(x² - 4x + 3) ≥ 0

• BXD
• KL: S = [-2;1] [3;+∞]

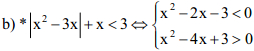
• Lập bảng xét dấu
• Tập nghiệm S = (-1;1)

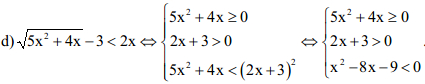
BXD

Câu 2.(1 điểm) Định m để bất phương trình sau luôn nghiệm đúng với mọi x thuộc R:

x² + 2(m + 1)x + 9m - 5 > 0

Bất phương trình nghiệm đúng với mọi x thuộc R

Câu 3:

Gọi x, y lần lượt là số sản phẩm loại I và II mà xí nghiệp cần sản xuất.

Để sản xuất được x sản phẩm loại I và y sản phẩm loại II cần dùng:

• Nguyên liệu A: 2x + y (kg)
• Nguyên liệu B: x + 2y (kg)

Theo đề bài ta có hệ:

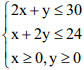
Lợi nhuận: F(x, y) = 8x + 6y (triệu đồng)

Vẽ miền nghiệm

F(x, y) đạt gtln tại 1 trong 4 đỉnh của tứ giác OABC

• Tại O(0;0) : F (0;0) = 0
• Tại A(0,12) : F(0,12) = 72
• Tại B(12,6) : F(12,6) = 132
• Tại C(15,0) : F(15,0) = 120

Vậy F(x, y) đạt gtln tại B(12;6) tức là cần sản xuất 12 sản phẩm loại I và 6 sản phẩm loại II thì đạt được lợi nhuận cao nhất.

(Còn tiếp)