Đề thi giữa kì 1 Toán 9 năm học 2022 - 2023 - Đề 1

Đề thi giữa học kì 1 Toán 9 năm học 2022 - 2023

Đề kiểm tra giữa kì 1 Toán 9 – Đề số 1
Đáp án đề thi giữa học kì 1 Toán 9 – Đề số 1

Đề thi giữa kì 1 Toán 9 năm 2022 được Tìm Đáp Án biên soạn là đề thi hay và chất lượng cho các bạn học sinh tham khảo củng cố kiến thức. Đề kiểm tra giữa kì 1 Toán 9 bao gồm 4 câu hỏi tự luận có đáp án, cho các em luyện tập, so sánh và đối chiếu với bài làm của mình, giúp các em rèn luyện kỹ năng giải Toán, chuẩn bị cho bài thi giữa học kì 1 lớp 9 đạt kết quả cao. Mời các em học sinh tham khảo chi tiết.

Tham khảo thêm: Đề thi giữa học kì 1 lớp 9 môn Toán năm học 2022 - 2023 - Đề số 2

Bản quyền thuộc về Tìm Đáp Án.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

Đề kiểm tra giữa kì 1 Toán 9 – Đề số 1

Bài 1 (3 điểm): Cho biểu thức:

$P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$

a) Tìm điều kiện của x để biểu thức P có nghĩa?

b) Rút gọn biểu thức

c) Tìm giá trị x nguyên để P nhận giá trị nguyên

Bài 2 (2 điểm): Tính giá trị của biểu thức:

a) $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$

b) $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

Bài 3 (2 điểm): Giải phương trình:

a) ${x^2} - 4x - 45 = 0$

b) $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}$

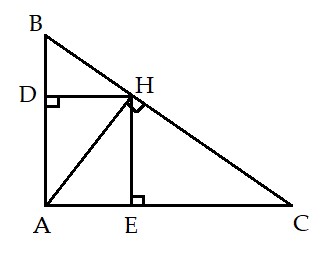
Bài 4 (3 điểm): Cho tam giác ABC (AB < AC) có $\widehat B + \widehat C = {90^0}$ , AH là đường cao xuất phát từ đỉnh A (H ∈ BC). Gọi D là hình chiếu của H lên AB (D ∈ AB) và E là hình chiếu của H lên AC (E ∈ AC).

a) Chứng minh ADHE là hình chữ nhật

b) Chứng minh AD.AB = AE.AC

c) Biết AB = 6cm và AC = 8cm. Tính độ dài BC, AH, AD và AE

Đáp án đề thi giữa học kì 1 Toán 9 – Đề số 1

Bài 1:

a) Để P có nghĩa

b) $P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$

$P = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{{2\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - \frac{{3x - 8\sqrt x + 27}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$

$P = \frac{{x + 3\sqrt x + 2\sqrt x + 6 + 2x - 6\sqrt x - \left( {3x - 8\sqrt x + 27} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$

$P = \frac{{7\sqrt x - 21}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{{7\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{7}{{\sqrt x + 3}}$

Vậy $P = \frac{7}{{\sqrt x + 3}}$

c) Để P nhận giá trị nguyên

Ta có bảng:

$\sqrt x + 3$	- 7	- 1	1	7
$\sqrt x$	- 10 (loại)	- 4 (loại)	- 2 (loại)	4
x				16 (tm)

Vậy để P nhận giá trị nguyên thì x = 16.

Bài 2:

a) $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$

$A = \sqrt {1 - 2.1.2\sqrt 3 + 12} + \sqrt {1 + 2.1.2\sqrt 3 + 12}$

$A = \sqrt {{{\left( {1 - 2\sqrt 3 } \right)}^2}} + \sqrt {{{\left( {1 + 2\sqrt 3 } \right)}^2}}$

$A = 2\sqrt 3 - 1 + 1 + 2\sqrt 3 = 4\sqrt 3$

b) $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\sqrt 6 \left( {\sqrt 2 - \sqrt 3 } \right)}}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \sqrt 2 - \sqrt 3 + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\left( {\sqrt 2 - \sqrt 3 } \right)\left( {\sqrt 2 + \sqrt 3 } \right) + 1}}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\left( {2 - 3} \right) + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{{ - 1 + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{0}{{\sqrt 2 + \sqrt 3 }} = 0$

Bài 3:

a) ${x^2} - 4x - 45 = 0$

$\Leftrightarrow {x^2} - 9x + 5x - 45 = 0$

$\Leftrightarrow x\left( {x - 9} \right) + 5\left( {x - 9} \right) = 0$

$\Leftrightarrow \left( {x + 5} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x + 5 = 0\\ x - 9 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 5\\ x = 9 \end{array} \right.$

Vậy S = {-5; 9}

b) $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\left( {x \ge 0;x \ne 9} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\left( {\sqrt x + 3} \right) - \left( {\sqrt x - 3} \right)\left( {\sqrt x - 3} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - \left( {x - 6\sqrt x + 9} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - x + 6\sqrt x - 9$

$\Leftrightarrow x - 5\sqrt x + 4 = 0$

$\Leftrightarrow x - \sqrt x - 4\sqrt x + 4 = 0$

$\Leftrightarrow \sqrt x \left( {\sqrt x - 1} \right) - 4\left( {\sqrt x - 1} \right) = 0$

$\Leftrightarrow \left( {\sqrt x - 4} \right)\left( {\sqrt x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} \sqrt x = 4\\ \sqrt x = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 16\\ x = 1 \end{array} \right.\left( {tm} \right)$

Vậy S = {1; 16}

Bài 4:

Đề thi giữa học kì 1 Toán 9 năm học 2020 - 2021 - Đề 1

a) + Xét tam giác ABC có: $\widehat A + \widehat B + \widehat C = {180^0}$ (tổng ba góc trong tam giác)

mà $\widehat B + \widehat C = {90^0} \Rightarrow \widehat A = {90^0}$

+ Xét tứ giác ADHE có:

$\widehat {DAE} = {90^0}$ (cmt)

$\widehat {HDA} = {90^0}$ ( $HD \bot AB$ - gt)

$\widehat {HEA} = {90^0}$ ( $HE \bot AC$ - gt)

$\Rightarrow$ ADHE là hình chữ nhật (dhnb) (đpcm)

b) + Xét tam giác ABH có $\widehat {AHB} = {90^0};HD \bot AB$ :

$A{H^2} = AD.AB$ (hệ thức lượng trong tam giác vuông) (1)

+ Xét tam giác AHC có $\widehat {AHC} = {90^0};HE \bot AC$ :

$A{H^2} = AE.AC$ (hệ thức lượng trong tam giác vuông) (2)

+ Từ (1) và (2) $\Rightarrow AD.AB = AE.AC\left( { = A{H^2}} \right)$ (đpcm)

c) + Xét tam giác ABC có $\widehat {BAC} = {90^0};AH \bot BC$ :

$A{B^2} + A{C^2} = B{C^2}$ (Pitago)

$\Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {100} = 10$ (cm)

$\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow AH = \sqrt {\frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}}} = \frac{{24}}{5}$ (cm)

+ Từ (1) $\Rightarrow AD = \frac{{A{H^2}}}{{AB}} = \frac{{96}}{{25}}$ (cm)

+ Từ (2) $\Rightarrow AE = \frac{{A{H^2}}}{{AC}} = \frac{{72}}{{25}}$ (cm)

---------------

Nhằm mang đến cho các em học sinh nguồn tài liệu hữu ích ôn thi giữa kì 1, TimDapAngiới thiệu chuyên mục Đề thi giữa kì 1 lớp 9 với đầy đủ các môn, giúp các em ôn luyện trước kì thi, đồng thời cũng là tài liệu hay cho thầy cô tham khảo ra đề.

Ngoài Đề kiểm tra giữa học kì 1 môn Toán lớp 9, các bạn học sinh còn có thể tham khảo các đề thi học kì 1 lớp 9, đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, TimDapAnmời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9 . Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Nếu bạn không thấy đề thi được hiển thị. Vui lòng tải về để xem. Nếu thấy hay thì các bạn đừng quên chia sẻ cho bạn bè nhé!

Tải về