Lý thuyết Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn Toán 12 Kết nối tri thức

1. Tốc độ thay đổi của một đại lượng

1. Tốc độ thay đổi của một đại lượng

- Nếu s = s(t) là hàm vị trí của một vật chuyển đọng trên một đường thẳng thì v = s’(t) biểu thị vận tốc tức thời của vật. Tốc độ thay đổi tức thời của vận tốc theo thời gian là gia tốc tức thời của vật: a(t) = v’(t) = s’’(t)

- Nếu C = C(t) là nồng độ của một chất tham gia phản ứng hóa học tại thời điểm t, thì C’(t) là tốc độ phản ứng tức thời của chất đó tại thời điểm t

- Nếu P = P(t) là số lượng cá thể trong một quần thể động vật hoặc thực vật tại thời điểm t, thì P’(t) biểu thị tốc độ tăng trưởng tức thời của quần thể tại thời điểm t

- Nếu C = C(x) là hàm chi phí, tức là tổng chi phí khi sản xuất x đơn vị hàng hóa, thì tốc độ thay đổi tức thời C’(x) của chi phí đó đối với số lượng đơn vị hàng được sản xuất được gọi là chi phí biên

- Về ý nghĩa kinh tế, chi phí biên C’(x) xấp xỉ với chi phí để sản xuất thêm một đơn vị hàng hóa tiếp theo, tức là đơn vị hàng hóa thứ x + 1

Ví dụ: Khi bỏ qua sức cản của không khí, độ cao (mét) của một vật được phóng thẳng đứng lên trên từ điểm cách mặt đất 2m với vận tốc ban đầu 24,5 m/s là \(h(t) = 2 + 24,5t - 4,9{t^2}\)

a) Tìm vận tốc của vật sau 2s

b) Khi nào vật đạt độ cao lớn nhất và độ cao lớn nhất đó là bao nhiêu?

c) Khi nào thì vật chạm đất và vận tốc của vật lúc chạm đất là bao nhiêu?

Lời giải

a) Ta có: v = h’(t) = 24,5 – 9,8t (m/s)

Do đó v(2) = 24,5 – 9,8.2 = 4,9 (m/s)

b) Vì h(t) là hàm số bậc hai có hệ số a = -4,9 < 0 nên h(t) đạt giá trị lớn nhất tại \(t = - \frac{b}{{2a}} = 2,5s\). Khi đó, độ cao lớn nhất của vật là h(2,5) = 32,625 (m)

c) Vật chạm đất khi h = 0, tức là \(2 + 24,5t - 4,9{t^2} = 0\) hay \(t \approx 5,08s\)

Vận tốc của vật lúc chạm đất là v(5,08) = 24,5 – 9,8.5,08 = -25,284 (m/s)

Vận tốc âm chứng tỏ chiều chuyện động của vật là ngược chiều dương (hướng lên trên) của trục đã chọn

2. Một vài bài toán tối ưu hóa đơn giản

Quy trình giải một bài toán tối ưu hóa

Bước 1. Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng trong bài toán

Bước 2. Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số Q = Q(x)

Bước 3. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số Q = Q(x) bằng các phương pháp đã biết và kết luận

Ví dụ: Một nhà sản xuất cần làm những hộp đựng hình trụ có thể tích 1 lít. Tìm các kích thước của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất

Đổi 1 lít = 1000 cm³

Gọi r (cm) là bán kính đáy của hình trụ, h (cm) là chiều cao của hình trụ

Diện tích toàn phần của hình trụ là \(S = 2\pi {r^2} + 2\pi rh\)

Do thể tích của hình trụ là 1000 cm³nên ta có: \(V = \pi {r^2}h = 1000\) hay \(h = \frac{{1000}}{{\pi {r^2}}}\)

Do đó, diện tích toàn phần của hình trụ là \(S = 2\pi {r^2} + \frac{{2000}}{r},r > 0\)

Ta cần tìm r sao cho S đạt giá trị nhỏ nhất. Ta có:

\(S' = 4\pi r - \frac{{2000}}{{{r^2}}} = \frac{{4\pi {r^3} - 2000}}{{{r^2}}};S' = 0 \Leftrightarrow \pi {r^3} = 500 \Leftrightarrow r = \sqrt[3]{{\frac{{500}}{\pi }}}\)

BBT

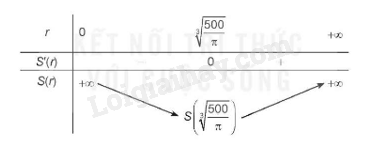
Khi đó: \(h = \frac{{1000}}{{\pi {r^2}}} = \frac{{100}}{{\sqrt[3]{{250\pi }}}}\)

Vậy cần sản xuất các hộp đựng hình trụ có bán kính đáy \(r = \sqrt[3]{{\frac{{500}}{\pi }}} \approx 5,42(cm)\) và chiều cao \(h = \frac{{100}}{{\sqrt[3]{{250\pi }}}} \approx 10,84(cm)\)

Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn Toán 12 Kết nối tri thức timdapan.com"