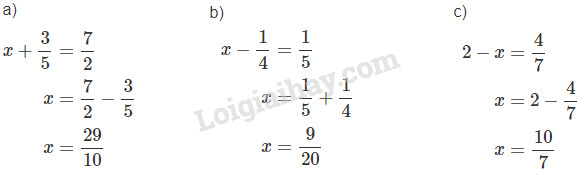Bài 13 : Luyện tập chung

Bài 1

Tính

\(a)\; \displaystyle {8 \over 5} + {3 \over {10}} = \;.....\)                           \(b) \; \displaystyle {2 \over 3} + {3 \over 4} + {1 \over 6} =\; .....\)

\( c)\;\displaystyle {5 \over 6} - {2 \over 9} = \;.....\)                             \( d) \;\displaystyle 2{1 \over {10}} - {3 \over 4} - {2 \over 5} =\; .....\)

Phương pháp giải:

- Muốn cộng (hoặc trừ) các phân số khác mẫu số ta quy đồng mẫu số rồi cộng (hoặc trừ) các phân số sau khi quy đồng.

- Biểu thức chỉ có phép cộng hoặc phép trừ thì tính lần lượt từ trái sang phải.

Lời giải chi tiết:

a) \( \displaystyle {8 \over 5} + {3 \over {10}} = {{16} \over {10}} + {3 \over {10}} = {{16 + 3} \over {10}} = {{19} \over {10}}\)

b) \( \displaystyle {2 \over 3} + {3 \over 4} + {1 \over 6} = {{8} \over {12}} + {{9} \over {12}} + {{2} \over {12}} \) \( \displaystyle = {{8 + 9 + 2} \over {12}} = {{19} \over {12}}\)

c) \( \displaystyle {5 \over 6} - {2 \over 9} = {{15} \over {18}} - {{4} \over {18}} = {{15 - 4} \over {18}} = {{11} \over {18}}\)

d) \( \displaystyle 2{1 \over {10}} - {3 \over 4} - {2 \over 5} = {{21} \over {10}} - {3 \over 4} - {2 \over 5}\)

\( \displaystyle = {{42} \over {20}} - {{15} \over {20}} - {{8} \over {20}}\) \( \displaystyle = {{42 - 15 - 8} \over {20}} = {{19} \over {20}}\)

Bài 2

Tìm \(x\) : 

\( \displaystyle a) \;x + {3 \over 5} = {7 \over 2}\)                    \( \displaystyle b)\;x - {1 \over 4} = {1 \over 5}\)                     \( \displaystyle c)\;2 - x = {4 \over 7}\)

Phương pháp giải:

Áp dụng các quy tắc :

- Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.

- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.

- Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.

Lời giải chi tiết:

Bài 3

viết các số đo độ dài (theo mẫu) : 

Mẫu: \( \displaystyle 9m\,3dm\, = \,9m + {3 \over {10}}m = 9{3 \over {10}}m\)

a) \( \displaystyle 2m \;2dm = ...................... \)

b) \( \displaystyle 12m\; 5dm = .....................\)

c) \( \displaystyle 15cm \;8mm = ...................\)

Phương pháp giải:

Áp dụng các cách đổi:

       \( \displaystyle 1m = 10dm\), hay  \( \displaystyle 1dm = \dfrac{1}{10}m\) ;

       \( \displaystyle 1cm = 10mm\), hay  \( \displaystyle  1mm = \dfrac{1}{10}cm\).

Lời giải chi tiết:

a) \( \displaystyle 2m\,2dm = \,2m + {2 \over 10}m = \,2m + {1 \over 5}m \) \( \displaystyle= 2{1 \over 5}m\) 

b) \( \displaystyle 12m\;5dm = 12m + {5 \over 10}m \)\( \displaystyle = 12m + {1 \over 2}m  \) \( \displaystyle= 12{1 \over 2}m\)

c) \( \displaystyle 15cm\,8mm = 15cm + {8 \over {10}}cm \)\( \displaystyle =15cm + {4 \over {5}}cm \)\( \displaystyle= 15{{4} \over {5}}cm\)

Bài 4

Biết \(\displaystyle  {7 \over {10}}\) số học sinh của một lớp học là \(21\) em. Hỏi lớp học đó có bao nhiêu học sinh?

Phương pháp giải:

- Tìm \( \dfrac{1}{10}\) số học sinh của lớp ta lấy \(21\) chia cho \(7\).

- Tìm số học sinh của lớp  ta lấy \( \dfrac{1}{10}\) số học sinh của lớp nhân với \(10\).

Lời giải chi tiết:

\( \dfrac{1}{10}\) số học sinh của lớp có số học sinh là :

                    \(21 : 7 = 3\) (học sinh)

Số học sinh của lớp học đó:

                     \(3 \times 10 = 30\) (học sinh)

                                   Đáp số: \(30\) học sinh.