Giải mục II trang 117, 118 SGK Toán 7 tập 2 - Cánh diều

II. Tính chất ba đường cao của tam giác

HĐ 2

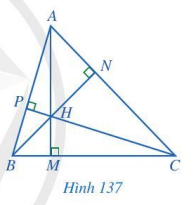
Quan sát ba đường cao AM, BN, CP của tam giác ABC (Hình 137), cho biết ba đường cao đó có cùng đi qua một điểm hay không.

Phương pháp giải:

Quan sát Hình 137 để xem ba đường cao AM, BN, CP có cùng đi qua một điểm hay không.

Lời giải chi tiết:

Ba đường cao AM, BN, CP có cùng đi qua một điểm là điểm H.

LT - VD 2

Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.

Phương pháp giải:

Chứng minh G là trực tâm của tam giác ABC bằng cách chứng minh G là giao điểm của ba đường cao của tam giác ABC.

Lời giải chi tiết:

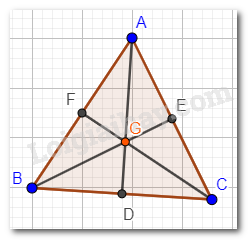
Tam giác ABC đều nên AB = AC = BC.

G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.

Suy ra: AF = BF = AE = CE = BD = CD.

Xét tam giác ADB và tam giác ADC có:

     AB = AC (tam giác ABC đều);

     AD chung

     BD = CD (D là trung điểm của đoạn thẳng BC).

Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).

Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)

Tương tự ta có:

\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)

\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)

Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.

Vậy G cũng là trực tâm của tam giác ABC.

LT - VD 3

Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.

Phương pháp giải:

Chứng minh AB = AC = BC

Lời giải chi tiết:

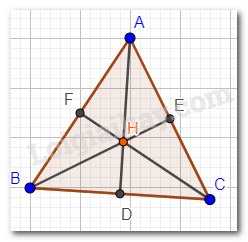
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.

Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.

Suy ra: AF = BF = AE = CE = BD = CD;

\(AD \bot BC; BE \bot AC; CF \bot AB\)

Xét tam giác ADB và tam giác ADC có:

     AD chung

    \(\widehat{ADB}=\widehat{ADC} (=90^0)\)

     BD = CD (D là trung điểm của đoạn thẳng BC).

Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).

Tương tự, ta cũng được, AC = BC

Xét tam giác ABC có AB = AC = BC nên là tam giác đều.

Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.