Giải bài 4 trang 118 SGK Toán 7 tập 2 - Cánh diều
Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H,
Đề bài
Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, \(\widehat {HCA} = 25^\circ \). Tính \(\widehat {BAC}\)và \(\widehat {HBA}\).
Phương pháp giải - Xem chi tiết
Tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Lời giải chi tiết
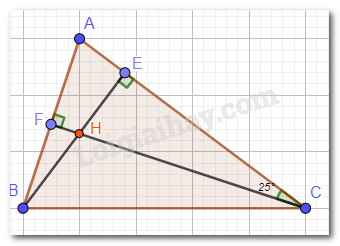
Xét tam giác AFC có: \(\widehat {HCA} = 25^\circ \); \(\widehat {AFC} = 90^\circ \) (vì CF vuông góc với AB).
Nên: \(\widehat {FAC} = \widehat {BAC} = 90^\circ - 25^\circ = 65^\circ \).
Xét tam giác AEB có: \(\widehat {BAC} = 65^\circ \); \(\widehat {AEB} = 90^\circ \)(vì BE vuông góc với AC).
Nên: \(\widehat {ABE} = \widehat {HBA} = 90^\circ - 65^\circ = 25^\circ \).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 118 SGK Toán 7 tập 2 - Cánh diều timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 118 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







