Giải mục I trang 74, 75 SGK Toán 7 tập 2 - Cánh diều
I. Quan hệ giữa góc và cạnh đối diện trong một tam giác
I. Quan hệ giữa góc và cạnh đối diện trong một tam giác
HĐ 1
Quan sát tam giác ABC ở Hình 17.
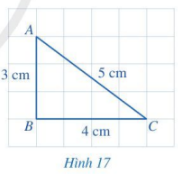
a) So sánh hai cạnh AB và AC.
b) So sánh góc B (đối diện với cạnh AC) và góc C (đối diện với cạnh AB).
Phương pháp giải:
a) Dựa vào độ dài cạnh đã cho để so sánh hai cạnh AB và AC.
b) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
Lời giải chi tiết:
a) Trong tam giác ABC:
\(AB = 3\) cm, \(AC = 5\) cm.
Vậy AB < AC.
b) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
LT - VD 1
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
Phương pháp giải:
Góc lớn nhất trong tam giác là góc đối diện với cạnh lớn nhất trong tam giác.
Góc nhỏ nhất trong tam giác là góc đối diện với cạnh nhỏ nhất trong tam giác.
Lời giải chi tiết:
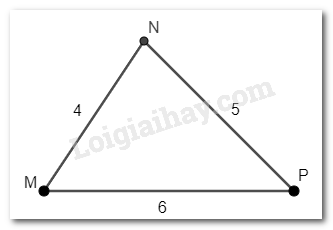
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)
HĐ 2
Quan sát tam giác ABC ở Hình 19.
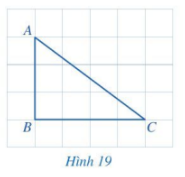
a) So sánh hai góc B và C.
b) So sánh cạnh AB (đối diện với góc C) và cạnh AC (đối diện với góc B).
Phương pháp giải:
a) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
b) Học sinh có thể dùng thước kẻ (có chia vạch đo) để so sánh hai cạnh hoặc dựa vào độ dài được kẻ của các cạnh trên hình (mỗi một cạnh ô vuông là 1 cm).
Lời giải chi tiết:
a) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
b) Ta có: \(AB = 3\)cm, \(AC = 5\) cm. Vậy AB < AC.
LT - VD 2
a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.
b) Cho tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.
Phương pháp giải:
a) So sánh hai góc đối diện với hai cạnh để so sánh hai cạnh. (Góc đối diện với cạnh lớn hơn thì cạnh lớn hơn)
b) Cạnh nhỏ nhất trong tam giác là cạnh đối diện với góc nhỏ nhất trong tam giác.
Cạnh lớn nhất trong tam giác là cạnh đối diện với góc lớn nhất trong tam giác.
Lời giải chi tiết:
a)
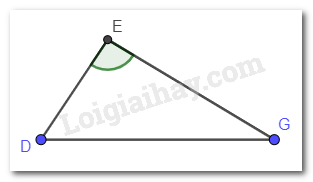
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.
Vậy DE < DG.
b)
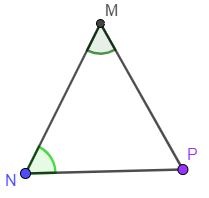
Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ - 56^\circ - 65^\circ = 59^\circ \).
Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục I trang 74, 75 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







