Giải mục 3 trang 86, 87 SGK Toán 9 tập 2 - Chân trời sáng tạo
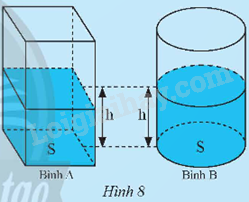
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình. a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B. b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 86 SGK Toán 9 Chân trời sáng tạo
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình.
a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B.
b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r và h.
Phương pháp giải:
Dựa vào dữ kiện đề bài rồi biến đổi theo S, h và r.
Lời giải chi tiết:
a) Thể tích V của lượng nước trong bình A là: V = S.h
Thể tích V của lượng nước trong bình B là: V = S.h
b) Thể tích V của lượng nước trong bình B là: V = S.h = \(\pi \)r2h.
TH3
Trả lời câu hỏi Thực hành 3 trang 87 SGK Toán 9 Chân trời sáng tạo
Phần bên trong của một cái bể hình trụ có chiều cao 2,1 m và bán kính đáy 1,5 m. Tính thể tích lượng nước trong bể biết mực nước bằng \(\frac{2}{3}\)chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
Phương pháp giải:
Dựa vào công thức tính thể tích của hình trụ: V = S.h = \(\pi \)r2h
Lời giải chi tiết:
Thể tích của bể là: V = \(\pi \)r2h = \(\pi \).1,52.2,1 = 4,725\(\pi \) (m3).
Thể tích lượng nước trong bể là:
\(V' = \frac{2}{3}V = \frac{2}{3}.4,725\pi \) = 10 (m3).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 86, 87 SGK Toán 9 tập 2 - Chân trời sáng tạo timdapan.com"







