Giải mục 3 trang 67, 68 SGK Toán 11 tập 1 - Chân trời sáng tạo

Hoạt động 4

Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại và cứ tiếp tục như vậy (xem Hình 2).

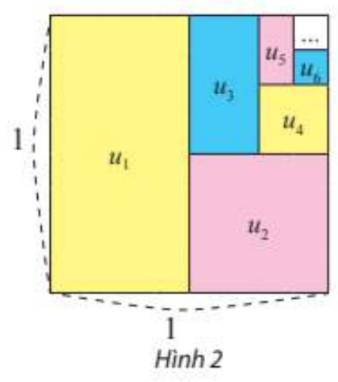
a) Xác định diện tích \({u_k}\) của phần hình được tô màu lần thứ \(k\left( {k = 1,2,3,...} \right)\).

b) Tính tổng diện tính \({S_n}\) của phần  hình được tô màu sau lần tô thứ \(n\left( {n = 1,2,3,...} \right)\).

c) Tìm giới hạn \(\lim {S_n}\) và so sánh giới hạn này với diện tích hình vuông ban đầu.

Phương pháp giải:

a) Dựa vào đề bài, ta đưa ra công thức tổng quát của \({u_k}\) dựa vào công thức số hạng tổng quát của cấp số nhân có số hạng đầu \({u_1}\) và công bội \(q\): \({u_k} = {u_1}.{q^{k - 1}}\).

b) Áp dụng công thức tính tổng \({S_n}\) của \(n\) số hạng đầu của cấp số nhân có số hạng đầu \({u_1}\) và công bội \(q\): \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}}\).

c) Áp dụng các phép toán về giới hạn hữu hạn của dãy số và công thức tính giới hạn cơ bản: \(\lim {q^n} = 0\), với \(q\) là số thực thỏa mãn \(\left| q \right| < 1\).

Lời giải chi tiết:

a) Theo đề bài, ta thấy \(\left( {{u_k}} \right)\) là cấp số nhân với số hạng đầu \({u_1} = \frac{1}{2}\), công bội \(q = \frac{1}{2}\).

Vậy \({u_k} = {u_1}.{q^{k - 1}} = \frac{1}{2}.{\left( {\frac{1}{2}} \right)^{k - 1}} = {\left( {\frac{1}{2}} \right)^k} = \frac{1}{{{2^k}}}\).

b) \(\left( {{u_n}} \right)\) là cấp số nhân với số hạng đầu \({u_1} = \frac{1}{2}\), công bội \(q = \frac{1}{2}\).

Vậy \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}} = \frac{1}{2}.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = \frac{1}{2}.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{\frac{1}{2}}} = 1 - {\left( {\frac{1}{2}} \right)^n}\).

c) \(\lim {S_n} = \lim \left( {1 - {{\left( {\frac{1}{2}} \right)}^n}} \right) = \lim 1 - \lim {\left( {\frac{1}{2}} \right)^n}\).

\(\lim 1 = 1\) vì 1 là hằng số.

\(\left| {\frac{1}{2}} \right| = \frac{1}{2} < 1\) nên \(\lim {\left( {\frac{1}{2}} \right)^n} = 0\)

Vậy \(\lim {S_n} = \lim 1 - \lim {\left( {\frac{1}{2}} \right)^n} = 1 - 0 = 1\)

Giới hạn này bằng diện tích của hình vuông ban đầu.

Thực hành 4

Tính tổng của cấp số nhân lùi vô hạn: \(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ...\).

Phương pháp giải:

Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)

Lời giải chi tiết:

Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{3}\) nên

\(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ... = \frac{1}{{1 - \frac{1}{3}}} = \frac{3}{2}\).

Vận dụng 1

Từ tờ giấy, cắt một hình tròn bán kính \(R\left( {cm} \right)\) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính \(\frac{R}{2}\) rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính \(\frac{R}{4}\) rồi chồng lên các hình trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.

Phương pháp giải:

Đưa tổng diện tích của các hình tròn về tổng của cấp số nhân lùi vô hạn rồi áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)

Lời giải chi tiết:

Giả sử các hình tròn bán kính \({R_1} = R,{R_2} = \frac{R}{2},{R_3} = \frac{R}{4} = \frac{R}{{{2^2}}},...,{R_n} = \frac{R}{{{2^{n - 1}}}},...\) có diện tích lần lượt là \({u_1},{u_2},{u_3},...,{u_n},...\) Ta có:

\(\begin{array}{l}{u_1} = \pi R_1^2 = \pi {R^2},{u_2} = \pi R_2^2 = \pi {\left( {\frac{R}{2}} \right)^2} = \pi {R^2}.\frac{1}{{{2^2}}},{u_3} = \pi R_3^2 = \pi {\left( {\frac{R}{{{2^2}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^4}}},...,\\{u_n} = \pi R_n^2 = \pi {\left( {\frac{R}{{{2^{n - 1}}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^{2n - 2}}}},...\end{array}\)

\(\begin{array}{l}S = {u_1} + {u_2} + ... + {u_n} + ... = \pi {R^2} + 2\pi {R^2}.\frac{1}{{{2^2}}} + 4.\pi {R^2}.\frac{1}{{{2^4}}} + ... + {2^{n + 1}}\pi {R^2}.\frac{1}{{{2^{2n - 2}}}} + ...\\\,\,\,\, = \pi {R^2} + \pi {R^2}.\frac{1}{2} + \pi {R^2}.\frac{1}{{{2^2}}} + ... + \pi {R^2}.\frac{1}{{{2^{n - 1}}}} + ...\\\,\,\,\, = \pi {R^2}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...} \right)\end{array}\)

Xét tổng: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...\)

Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{2}\) nên: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{2}}} = 2\).

Vậy \(S = \pi {R^2}.{S_n} = 2\pi {R^2}\).