Giải mục 2 trang 81, 82 SGK Toán 11 tập 2 - Cùng khám phá
Viết công thức tính thể tích khối chóp tam giác đều (Hình 8.72)
Hoạt động 2
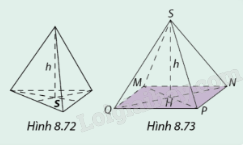
Viết công thức tính thể tích khối chóp tam giác đều (Hình 8.72) và khối chóp tứ giác đều (Hình 8.73) theo diện tích đáy S và chiều cao h của chúng.
Phương pháp giải:
\(V = \frac{1}{3}S.h\)
Lời giải chi tiết:
Công thức tính thể tích khối chóp: \(V = \frac{1}{3}S.h\)
Luyện tập 2
Cho hình chóp S.ABCD có đáy ABCD hình thoi cạnh a, \(\widehat {ABC} = {60^0}\), SB = a. Hình chiếu của S trên (ABCD) là giao điểm hai đường chéo của hình thoi ABCD. Tính thể tích khối chóp này.
Phương pháp giải:
Hình thoi có 2 đường chéo vuông góc với nhau.
Áp dụng công thức tính thể tích hình chóp: \(V = \frac{1}{3}S.h\)
Lời giải chi tiết:
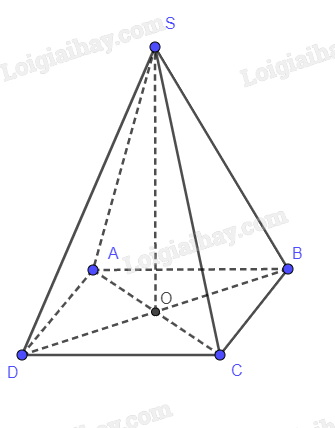
ABCD là hình thoi có cạnh bằng a. Mà \(\widehat {ABC} = {60^0}\) nên AC = a
AC và BD vuông góc với nhau tại O, ta có: \(BO = \sqrt {A{B^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{1}{2}a} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\)
\( \Rightarrow BD = \sqrt 3 a\)
O là hình chiếu của S trên (ABCD) nên SO vuông góc với (ABCD)
Suy ra SO vuông góc với BD nên tam giác SOB vuông tại O
\( \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{\sqrt 3 }}{2}a} \right)}^2}} = \frac{1}{2}a\)
\(\begin{array}{l} \Rightarrow V = \frac{1}{3}S.h = \frac{1}{3}.\frac{1}{2}AC.BD.SO = \frac{1}{6}.a.\sqrt 3 a.\frac{1}{2}a\\ = \frac{{\sqrt 3 }}{{12}}{a^3}\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 81, 82 SGK Toán 11 tập 2 - Cùng khám phá timdapan.com"







