Giải mục 1 trang 73, 74 SGK Toán 11 tập 2 - Cùng khám phá
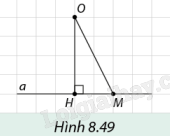
Cho đường thẳng a và một điểm O không thuộc a. H là hình chiếu của O trên đường thẳng a và M là một điểm bất kì thuộc a (Hình 8.49).
Hoạt động 1
Cho đường thẳng a và một điểm O không thuộc a. H là hình chiếu của O trên đường thẳng a và M là một điểm bất kì thuộc a (Hình 8.49). Trong hai điểm H và M điểm nào có khoảng cách đến O ngắn hơn? Vì sao?
Phương pháp giải:
Quan hệ giữa đường xiên và hình chiếu.
Lời giải chi tiết:
Trong điểm H và M thì điểm H gần O hơn.
Vì tam giác OHM vuông tại H nên ta có OH < OM (quan hệ giữa đường xiên và hình chiếu)
Luyện tập 1
Cho hình lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC. Tính khoảng cách từ G đến đường thẳng A’C’.
Phương pháp giải:
Cho O không thuộc a. H là hình chiếu của O trên a. Độ dài OH là khoảng cách từ O đến a.
Lời giải chi tiết:
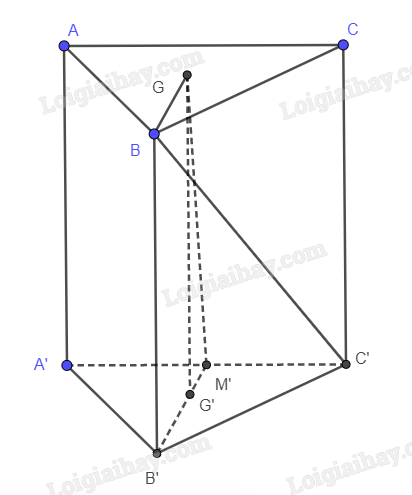
Gọi G’ là trọng tâm tam giác A’B’C’, M là trung điểm AC, M’ là trung điểm của A’C’
Ta có: GG’ vuông góc với (A’B’C’) nên GG’ vuông góc với A’C’
G’M’ là trung tuyến của A’B’C’ nên G’M’ vuông góc với A’C’ (Vì tam giác A’B’C’ đều)
Suy ra (GG’M’) vuông góc với A’C’
\( \Rightarrow \)GM’ vuông góc với A’C’
Vậy GM’ là khoảng cách từ G đến A’C’
Tam giác A’B’C’ đều cạnh a nên B’M’ = \(B'M' = \frac{{\sqrt 3 }}{2}a\)
Suy ra G’M’ = \(G'M' = \frac{{\sqrt 3 }}{6}a\)
Xét tam giác vuông GM’G’ tại M’ có:
\(GM' = \sqrt {GG{'^2} + G'M{'^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{{\sqrt 3 }}{6}a} \right)}^2}} = \frac{{7\sqrt 3 }}{6}a\)
Hoạt động 2
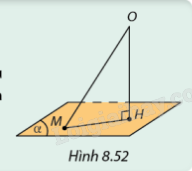
Cho mặt phẳng \(\left( \alpha \right)\) và O là một điểm không thuộc \(\left( \alpha \right)\). H là hình chiếu của O trên \(\left( \alpha \right)\). Lấy tuy ý điểm M thuộc \(\left( \alpha \right)\). Trong các diểm H và M, điểm nào có khoảng cách đến O ngắn hơn? Vì sao?
Phương pháp giải:
Quan hệ đường xiên và hình chiếu.
Lời giải chi tiết:
Tam giác OHM vuông tại H nên OH < OM (Quan hệ đường xiên và hình chiếu).
Luyện tập 2
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = 2a; tam giác ABC đều bằng a. Tính khoảng cách từ A đến mặt phẳng (SBC).
Phương pháp giải:
Tìm khoảng cách từ M đến (P):
+ Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d.
+ Từ M hạ MH vuông góc với d (H thuộc d).
+ Khi đó MH chính là khoảng cách cần tìm.
Lời giải chi tiết:
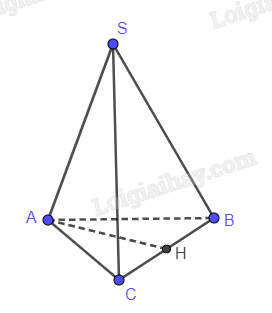
Gọi H là trung điểm của BC
Tam giác ABC đều nên AH vuông góc với BC
Suy ra \(d\left( {A,\left( {SBC} \right)} \right) = AH\)
\(AH = \sqrt {A{C^2} - C{H^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = \sqrt 3 a\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 73, 74 SGK Toán 11 tập 2 - Cùng khám phá timdapan.com"