Giải mục 1 trang 53 SGK Toán 11 tập 2 - Cùng khám phá
Trong không gian, cho hai đường thẳng (a,b).
Hoạt động 1
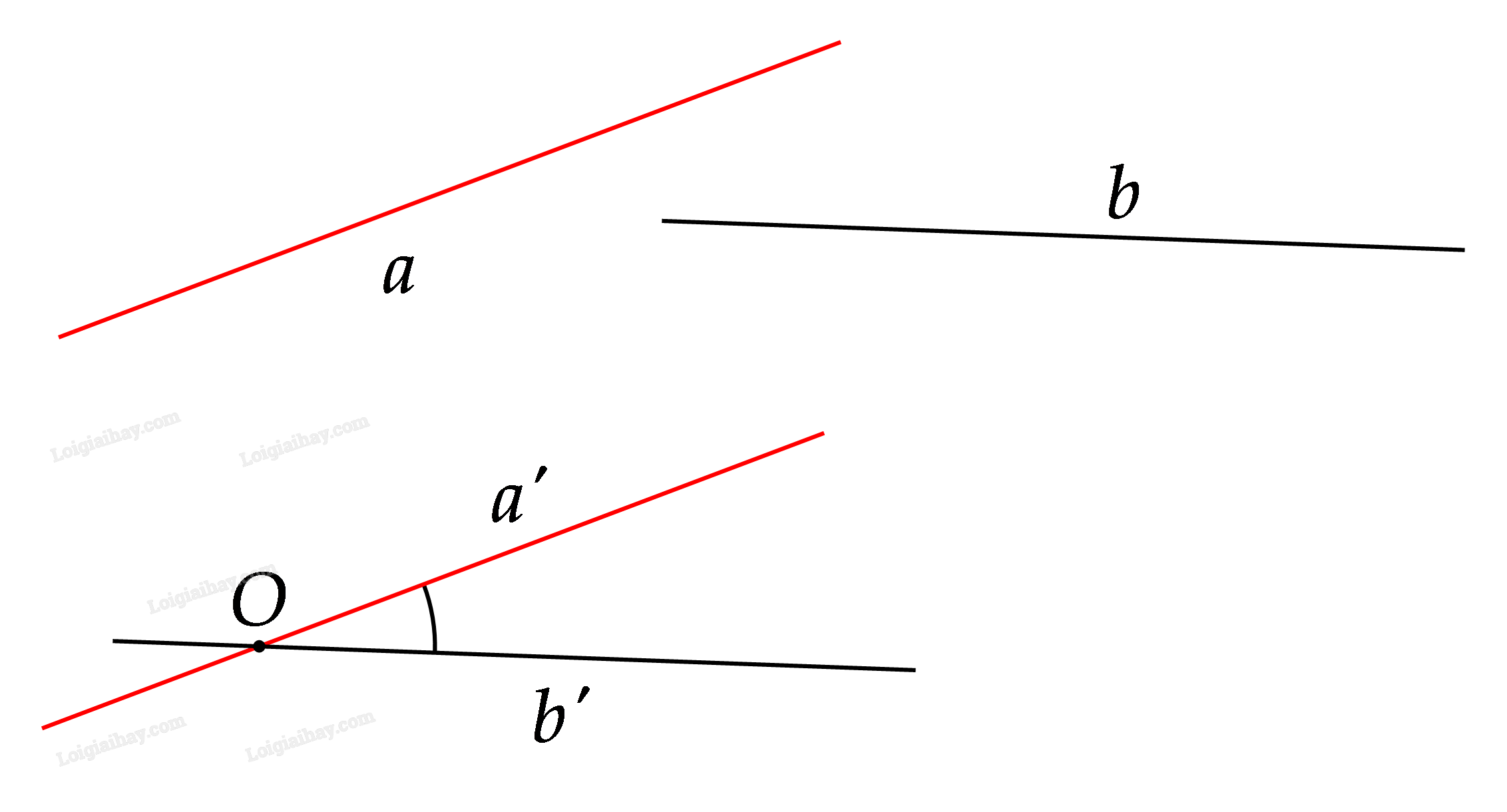
Trong không gian, cho hai đường thẳng \(a,b\). Từ một điểm \(O\) lấy tùy ý, vẽ hai đường thẳng \(a',b'\) lần lượt song song (hoặc trùng) với \(a,b\) (Hình 8.1). Có nhận xét gì về góc giữa \(a'\) và \(b'\) khi \(O\) thay đổi?
Phương pháp giải:
Góc giữa hai đường thẳng trong khoảng từ \({0^o}\) đến \({90^o}\)
Lời giải chi tiết:
Góc giữa \(a'\) và \(b'\) không thay đổi khi \(O\) thay đổi và luôn bằng góc giữa \(a\) và \(b\)
Luyện tập 1
Cho hình lăng trụ \(ABC.A'B'C'\), biết tam giác \(ABC\) vuông cân tại \(A\). Tính các góc \(\left( {A'C';BC} \right),\) \(\left( {A'B',AC} \right)\), \(\left( {A'A;B'B} \right)\)
Phương pháp giải:
Để xác định góc giữa hai đường thẳng \(a,b\) ta có thể lấy điểm \(O\) thuộc đường thẳng \(a\) kẻ đường thẳng \(b'\) song song với \(b\). Khi đó \(\left( {a,b} \right) = \left( {a,b'} \right)\)
Nếu \(a//b\) hoặc \(a \equiv b\) thì \(\left( {a,b} \right) = {0^o}\)
Lời giải chi tiết:

+) Ta có \(AC//A'C'\) \( \Rightarrow \left( {A'C',BC} \right) = \left( {AC,BC} \right)\). Mà \(\Delta ABC\) vuông cân tại \(A\) nên \(\widehat {ACB} = {45^o}\). Vậy \(\left( {A'C',BC} \right) = \left( {AC,BC} \right) = \widehat {ACB} = {45^o}\)
+) Ta có \(A'B'//AB\) nên \(\left( {A'B',AC} \right) = \left( {AB,AC} \right)\). Mà \(\Delta ABC\) vuông cân tại \(A\) nên \(\widehat {CAB} = {90^o}\). Vậy \(\left( {A'B',AC} \right) = \left( {AB,AC} \right) = \widehat {CAB} = {90^o}\)
+) Ta có \(A'A//B'B\) nên \(\left( {A'A,B'B} \right) = {0^o}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 53 SGK Toán 11 tập 2 - Cùng khám phá timdapan.com"







