Giải mục 1 trang 51, 52 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ1

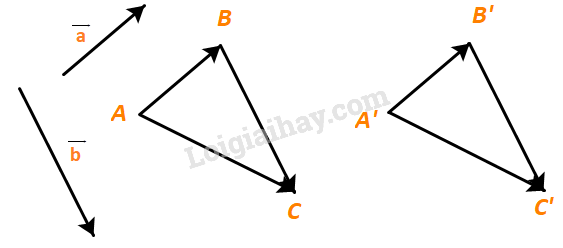
Với hai vectơ \(\overrightarrow a ,\overrightarrow b \) cho trước, lấy một điểm A vẽ các vectơ \(\overrightarrow {AB}  = \overrightarrow a ,\;\overrightarrow {BC}  = \overrightarrow b \). Lấy điểm A’ khác A và cũng vẽ các vectơ \(\overrightarrow {A'B'}  = \overrightarrow a ,\;\overrightarrow {B'C'}  = \overrightarrow b \). Hỏi hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) có mối quan hệ gì?

Phương pháp giải:

Hai vectơ bằng nhau nếu chúng có cùng độ dài và cùng hướng.

Xét độ dài và hướng của hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) để suy ra mối quan hệ của chúng.

Lời giải chi tiết:

\(\overrightarrow {AB}  = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}AB//\;a\\AB = a\end{array} \right.\) và \(\overrightarrow {A'B'}  = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}A'B'\;//\;a\\A'B' = a\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}AB//\;A'B'\\AB = A'B'\end{array} \right.\)

Tương tự, ta cũng suy ra \(\left\{ \begin{array}{l}BC//\;B'C'\\BC = B'C'\end{array} \right.\)

\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c-g-c)

\(\left\{ \begin{array}{l}AC//\;A'C'\\AC = A'C'\end{array} \right.\)

Dễ dàng suy ra  \(\overrightarrow {AC}  = \overrightarrow {A'C'} \).

HĐ2

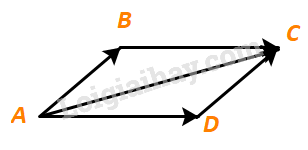
Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB}  + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)

Phương pháp giải:

Bước 1: Xác định vectơ \(\overrightarrow {AB}  + \overrightarrow {AD} \) bằng cách thay vectơ \(\overrightarrow {AD} \) bởi vectơ bằng nó mà có điểm đầu là B.

Bước 2: So sánh với vectơ \(\overrightarrow {AC} \)

Lời giải chi tiết:

Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD}  = \overrightarrow {BC} \).

Do đó \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \).

HĐ3

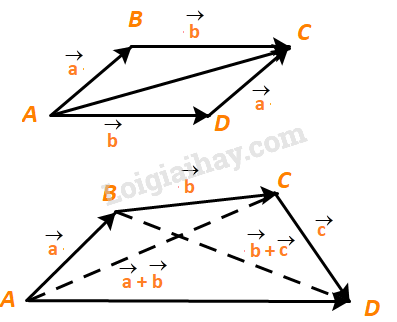
a) Trong hình 4.14a, hãy chỉ ra vectơ \(\overrightarrow a  + \overrightarrow b \)và vectơ \(\overrightarrow b  + \overrightarrow a \).

b) Trong hình 4.14b, hãy chỉ ra vectơ \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c \)và vectơ \(\overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\).

Phương pháp giải:

Nếu \(\overrightarrow {AB}  = \overrightarrow a ,\;\overrightarrow {BC}  = \overrightarrow b \) thì \(\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Lời giải chi tiết:

a) Ta có: \(\overrightarrow {AB}  = \overrightarrow a ,\;\overrightarrow {BC}  = \overrightarrow b \) nên \(\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Mặt khác: \(\overrightarrow {AD}  = \overrightarrow b ,\;\overrightarrow {DC}  = \overrightarrow a \) nên \(\overrightarrow b  + \overrightarrow a  = \overrightarrow {AD}  + \overrightarrow {DC}  = \overrightarrow {AC} \)

Do đó \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \).

b) Theo câu a) ta có \(\overrightarrow a  + \overrightarrow b  = \overrightarrow {AC} \) và \(\overrightarrow {CD}  = \overrightarrow c \) nên \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow {AC}  + \overrightarrow {CD}  = \overrightarrow {AD} \).

Mặt khác: \(\overrightarrow {BC}  = \overrightarrow b ,\;\overrightarrow {CD}  = \overrightarrow c \) nên \(\overrightarrow b  + \overrightarrow c  = \overrightarrow {BC}  + \overrightarrow {CD}  = \overrightarrow {BD} \)

Và \(\overrightarrow a  = \overrightarrow {AB} \) nên \(\overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right) = \overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD} \)

Vậy \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\)

Luyện tập 1

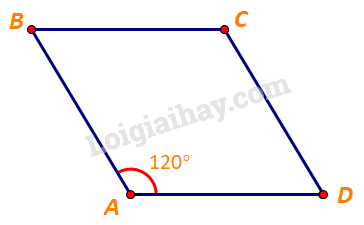
Cho hình thoi ABCD cới cạnh có độ dài bằng 1 và \(\widehat {BAD} = {120^o}\). Tính độ dài của các vectơ \(\overrightarrow {CB}  + \overrightarrow {CD} ,\;\overrightarrow {DB}  + \overrightarrow {CD}  + \overrightarrow {BA} .\)

Lời giải chi tiết:

\(\overrightarrow {CD}  = \overrightarrow {BA} \) do hai vectơ \(\overrightarrow {CD} ,\;\overrightarrow {BA} \) cùng hướng và \(CD = BA\).

\(\begin{array}{l} \Rightarrow \overrightarrow {CB}  + \overrightarrow {CD}  = \overrightarrow {CB}  + \overrightarrow {BA}  = \overrightarrow {CA} \\ \Leftrightarrow \left| {\overrightarrow {CB}  + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CA} } \right| = CA\end{array}\)

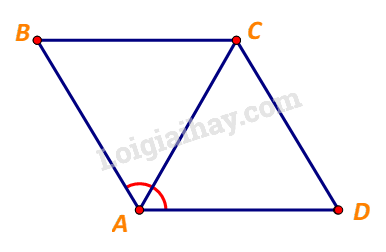
Xét tam giác ABC, ta có:

\(BA = BC\) và \(\widehat {BAC} = \frac{1}{2}.\widehat {BAD} = {60^o}\)

\( \Rightarrow \Delta ABC\) đều, hay \(CA = BC = 1\)

Vậy \(\left| {\overrightarrow {CB}  + \overrightarrow {CD} } \right| = 1.\)

Dựa vào tính chất kết hợp, ta có:

\(\begin{array}{l}\overrightarrow {DB}  + \overrightarrow {CD}  + \overrightarrow {BA}  = \left( {\overrightarrow {DB}  + \overrightarrow {CD} } \right) + \overrightarrow {BA} \\ = \left( {\overrightarrow {CD}  + \overrightarrow {DB} } \right) + \overrightarrow {BA}  = \overrightarrow {CB}  + \overrightarrow {BA}  = \overrightarrow {CA} .\\ \Rightarrow \left| {\overrightarrow {DB}  + \overrightarrow {CD}  + \overrightarrow {BA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = 1.\end{array}\)