Giải bài 4.10 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức

Đề bài

Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không khổi và có độ lớn bàng nhau. Hai tàu luôn dược giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yêu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước.

Lời giải chi tiết

Ta đã biết vectơ dòng nước và hướng di chuyển (tức là vectơ vận tốc thực của hai tàu).

Ta cần xác định vectơ vận tốc của mỗi tàu, chỉ biết chúng có độ lớn bằng nhau.

Giả sử tàu 1 là tàu đi về phía hạ lưu còn tàu 2 là tàu đi về phía thượng nguồn.

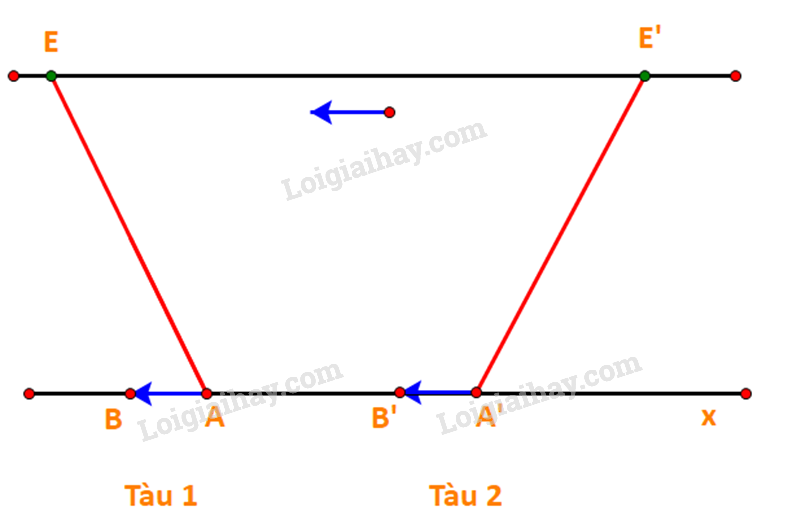
Tàu 1 và tàu 2 bắt đầu di chuyển từ điểm A và A’ ở bờ bên này đến điểm E, E’ ở bờ bên kia.

Vecto vận tốc dòng nước tác động lên tàu là như nhau, biểu diễn bởi các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {A'B'} \)

Gọi vectơ vận tốc riêng của hai tàu lần lượt là các vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {A'D'} \)

Vecto vận tốc thực của hai tàu là vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \).

Với tàu 1, để xác định các điểm C, D:

Từ B ta kẻ đường vuông góc với bờ, cắt AE tại một điểm, kí hiệu là C. Tiếp theo, dựng hình bình hành ABCD ta được điểm D.

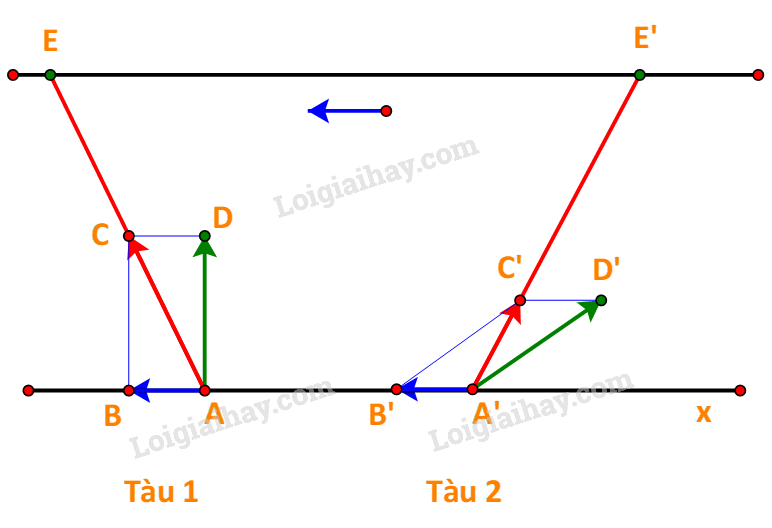
Với tàu 2, để xác định các điểm C’, D’

Trên A’E’ lấy điểm C’ sao cho B’C’= AD. Dựng hình bình hành A’B’C’D’, ta được điểm D’.

Giải thích:

Tàu 1: Được dòng nước đẩy theo vectơ \(\overrightarrow {AB} \), và đi với vận tốc thực là vectơ \(\overrightarrow {AD} \), khi ấy hướng di chuyển là vectơ tổng \(\overrightarrow {AB}  + \overrightarrow {AD} \) chính là vectơ \(\overrightarrow {AC} \)

Tàu 2: Bị dòng nước đẩy theo vectơ \(\overrightarrow {A'B'} \), và đi với vận tốc thực là vectơ \(\overrightarrow {A'D'} \), khi ấy hướng di chuyển là vectơ tổng \(\overrightarrow {A'B'}  + \overrightarrow {A'D'} \) chính là vectơ \(\overrightarrow {A'C'} \)

Các vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {A'D'} \)có độ dài bằng nhau (cùng bằng B’C’).

Do hai tàu chuyển động theo hướng tạo với bờ cùng một góc nhọn nên quãng đường đường đi khi chạm bờ bên kia là như nhau. Hay AE = A’E’.

Tàu nào có độ lớn vận tốc thực lớn hơn thì tàu đó sang bờ bên kia trước.

Xét tam giác A’B’C’, theo định lí cosin ta có:

\(A'C{'^2} = A'B{'^2} + B'C{'^2} - 2A'B'.B'C'.\cos B'\)

Mà \({0^o} < \widehat {B'} < \widehat {C'A'x} < {90^o} \Rightarrow \cos B' > 0\)

\( \Rightarrow A'C{'^2} < A'B{'^2} + B'C{'^2}\)

Mặt khác, tam giác ABC vuông tại B nên: \(A{C^2} = A{B^2} + B{C^2} = A{B^2} + A{D^2}\)

\( \Rightarrow A'C{'^2} < A{C^2}\) hay \(A'C' < AC\)

Vậy vận tốc của tàu 1 lớn hơn, nói cách khác tàu đi hướng xuống hạ lưu sẽ sang bờ bên kia trước.