Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức
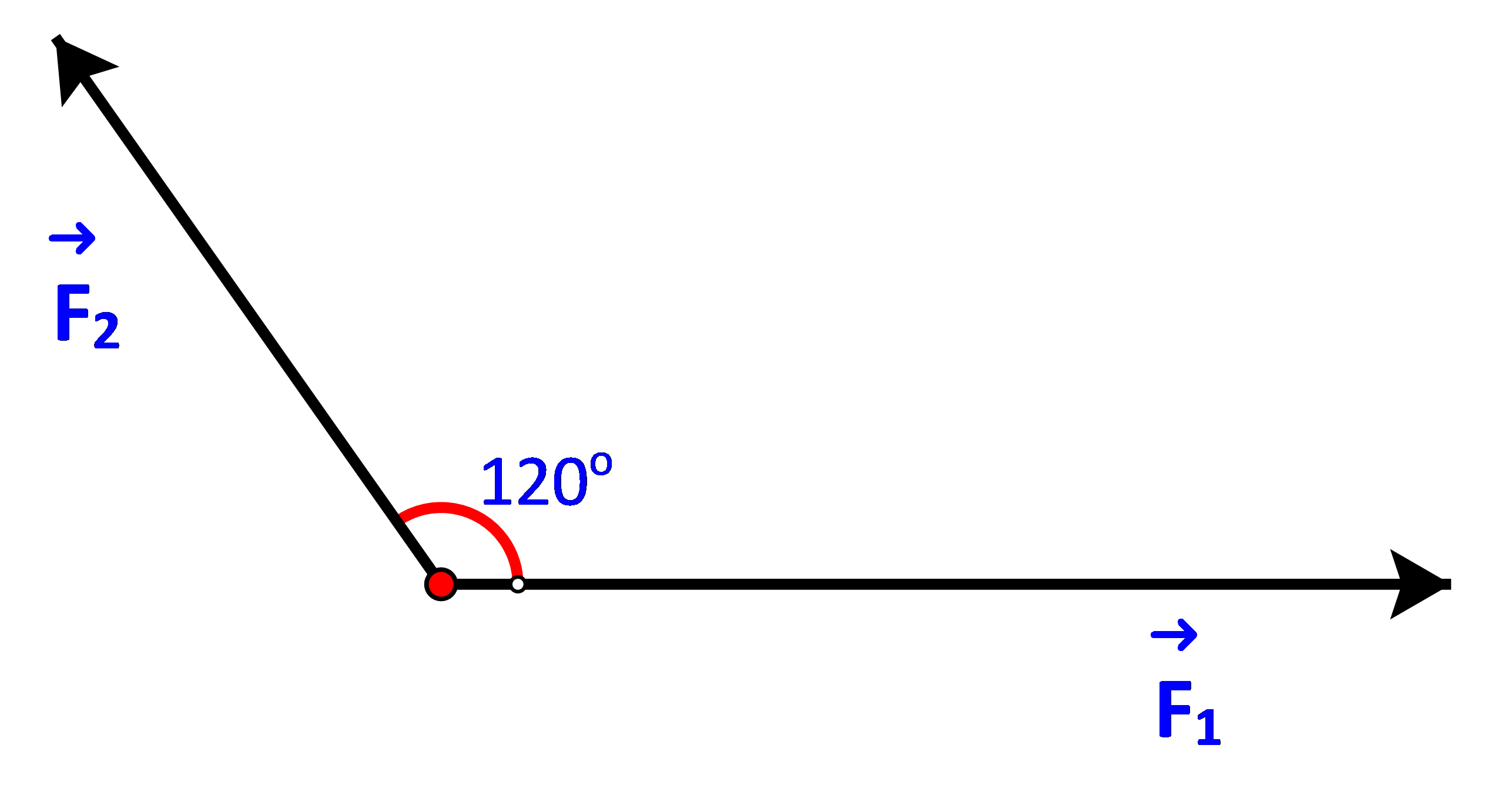
Hình 4.19 biểu diễn hai lực F1, F2 cùng tác động lên một vật, cho
Đề bài
Hình 4.19 biểu diễn hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, cho \(\left| {\overrightarrow {{F_1}} } \right| = 3\;N,\;\left| {\overrightarrow {{F_2}} } \right| = 2\;N.\) Tính độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).
Phương pháp giải - Xem chi tiết
Để tìm tổng của hai vectơ chung gốc \(\overrightarrow {AB} ,\;\overrightarrow {AC} \) ta dựng hình hình hành ABDC, khi đó:\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Lời giải chi tiết
Dựng hình bình hành ABDC với hai cạnh là hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) như hình vẽ
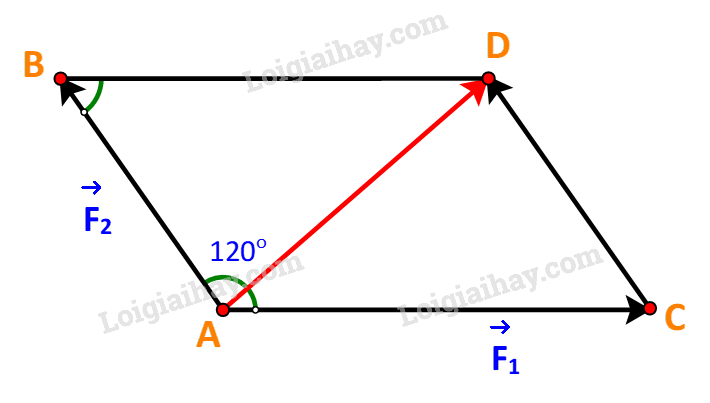
Ta có:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AC} + \overrightarrow {AB} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Xét \(\Delta ABD\) ta có:
\(BD = AC = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.\)
\(\widehat {ABD} = {180^o} - \widehat {BAC} = {180^o} - {120^o} = {60^o}\)
Theo định lí cosin ta có:
\(\begin{array}{l}A{D^2} = A{B^2} + B{D^2} - 2.AB.BD.\cos \widehat {ABD}\\ \Leftrightarrow A{D^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{D^2} = 7\\ \Leftrightarrow AD = \sqrt {7} \end{array}\)
Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {7} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức timdapan.com"







