Bài tập trắc nghiệm trang 190, 191 SBT Đại số 10

Chọn đáp án đúng:

6.37

Cho 0 < α < π/2. Biểu thức \(S = \dfrac{{\sin 4\alpha  - 2\sin 2\alpha }}{{\sin 4\alpha  + 2\sin 2\alpha }}\) có thể rút gọn thành biểu thức nào sau đây?

    A. -tan²α                   B. tanα

    C. cot²α                   D. cotα

Lời giải chi tiết:

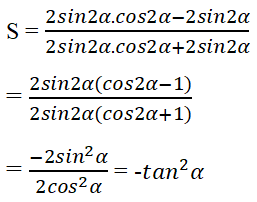
Đáp án: A

Ta cũng có thể suy luận cos2α – 1 < 0, cos2α + 1 > 0 nên S < 0, do đó các phương án B, C, D bị loại. Vậy đáp án là A.

6.38

Cho tan2a = 4/3 với π/2 < a < π. Giá trị cos a là

Lời giải chi tiết:

Cách 1. Tính trực tiếp:

Vì π/2 < a < π nên tan a < 0, do đó tan a = -2.

Áp dụng công thức

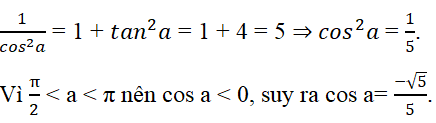
Đáp án là B.

Cách 2. Suy luận

Vì π/2 < a < π nên cos a < 0, do đó các phương án A, C, D bị loại.

Đáp án: B

6.39

Biết sin2a = -4/5 với 3π/4 < a < π. Giá trị tan a là

    A. 1/2          B. 2

    C. -2          D. -1/2

Lời giải chi tiết:

Cách 1. Tính trực tiếp.

Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.

Cách 2. Suy luận

Với 3π/4 < a < π thì -1 < tan a < 0, nên các phương án A, B, C đều bị loại.

Đáp án: D

6.40

Cho tanα = 2cotα và 3π/2 < α < 2π. Giá trị của biểu thức sinα + cosα là

Lời giải chi tiết:

Cách 1. Tính trực tiếp

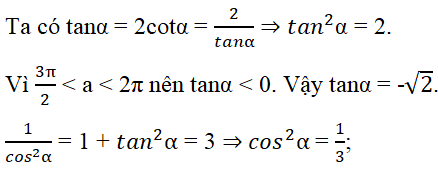
Do đó cosα = √3/3 (vì cosα > 0).

Suy ra sinα = tanα.cosα = (-√6)/3.

Vậy sinα + cosα = (√3- √6)/3. Đáp án là B.

Cách 2. Suy luận

Vì tanα = 2cotα và 3π/2 < α < 2π nên 3π/2 < α < 7π/4.

Do đó sinα < (-√2)/2 và cosα < √2/2.

Vì vậy sinα + cosα < 0.

Suy ra các phương án A, C, D bị loại.

Đáp án: B

6.41

Biết sinα - cosα = 1/2 và π < α < 5π/4. Giá trị cot2α là

Lời giải chi tiết:

Cách 1. Tính trực tiếp

Ta có (sinα – cosα)² = 1/4 = 1 – sin2α ⇒ sin2α = 3/4.

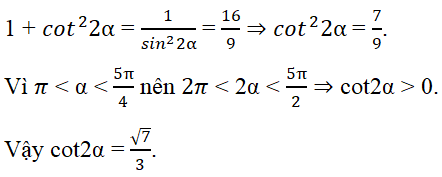
Đáp án là D.

Cách 2. Suy luận

Vì π < α < 5π/4 nên 2π < 2α < 5π/2. Suy ra cot2α > 0. Do đó các phương án A, B, C đều bị loại.

Đáp án: D