Giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức
Cho tứ diện ABCD, lấy hai điểm M, N thỏa mãn \(\overrightarrow {MB} + 2\overrightarrow {MA} = \overrightarrow 0 \) và \(\overrightarrow {NC} = 2\overrightarrow {DN} \). Hãy biểu diễn \(\overrightarrow {MN} \) theo \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
Đề bài
Cho tứ diện ABCD, lấy hai điểm M, N thỏa mãn \(\overrightarrow {MB} + 2\overrightarrow {MA} = \overrightarrow 0 \) và \(\overrightarrow {NC} = 2\overrightarrow {DN} \). Hãy biểu diễn \(\overrightarrow {MN} \) theo \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết
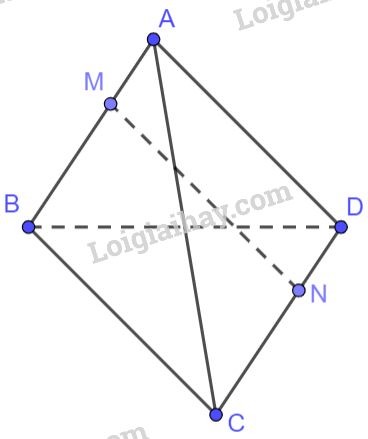
Ta có: \(\overrightarrow {MB} + 2\overrightarrow {MA} = \overrightarrow 0 \Rightarrow \overrightarrow {MB} = - 2\overrightarrow {MA} ,\overrightarrow {NC} = 2\overrightarrow {DN} \Rightarrow \overrightarrow {CN} = - 2\overrightarrow {ND} \)
Ta có: \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \) (1)
\(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} = - 2\overrightarrow {MA} + \overrightarrow {BC} - 2\overrightarrow {DN} \) (2)
Cộng vế với vế của (1) và (2) ta có:
\(2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} - 2\overrightarrow {MA} + \overrightarrow {BC} - 2\overrightarrow {DN} = - \overrightarrow {MA} - \overrightarrow {DN} + \overrightarrow {BC} + \overrightarrow {AD} \)
\( = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {AD} = \frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {CB} + \overrightarrow {CA} + \overrightarrow {AD} } \right) + \overrightarrow {BC} + \overrightarrow {AD} = \frac{2}{3}\overrightarrow {BC} + \frac{4}{3}\overrightarrow {AD} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức timdapan.com"







