Giải bài tập 10 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức
Cho hình hộp ABCD.A’B’C’D’ có tâm O và gọi G là trọng tâm của tam giác BDA’. Tỉ số \(\frac{{AG}}{{AO}}\) bằng A. \(\frac{1}{3}\). B. \(\frac{1}{2}\). C. \(\frac{2}{3}\). D. \(\frac{3}{4}\).
Đề bài
Cho hình hộp ABCD.A’B’C’D’ có tâm O và gọi G là trọng tâm của tam giác BDA’. Tỉ số \(\frac{{AG}}{{AO}}\) bằng
A. \(\frac{1}{3}\).
B. \(\frac{1}{2}\).
C. \(\frac{2}{3}\).
D. \(\frac{3}{4}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trọng tâm của tam giác để tính: Nếu G là trọng tâm của tam giác ABC và I là trung điểm của BC thì \(\frac{{GA}}{{AI}} = \frac{2}{3}\)
Lời giải chi tiết
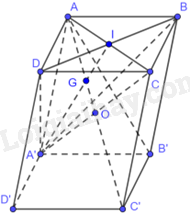
Gọi I là tâm của hình bình hành ABCD. Do đó, I là trung điểm của AC.
Vì G là trọng tâm của tam giác A’BD nên \(\frac{{A'G}}{{A'I}} = \frac{2}{3}\)
Tam giác A’AC có: A’I là đường trung tuyến và \(\frac{{A'G}}{{A'I}} = \frac{2}{3}\) nên G là trọng tâm của tam giác A’AC. Mà O là trung điểm của A’C (do O là tâm hình hộp ABCD.A’B’C’D’).
Do đó, \(\frac{{AG}}{{AO}} = \frac{2}{3}\)
Chọn C
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 10 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức timdapan.com"







