Bài II.8, II.9 trang 31 SBT Vật Lí 12

II.8

Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số \(50Hz\), được đặt tại hai điểm \({S_1}\) và \({S_2}\) cách nhau \(10cm\). Tốc độ truyền sóng trên mặt nước là \(75cm/s\). Xét các điểm trên mặt nước thuộc đường tròn tâm \({S_1}\), bán kính \({S_1}{S_2}\), điểm mà phân tử tại đó dao động với biên độ cực đại cách điểm \({S_2}\)một đoạn ngắn nhất bằng

A. \(8,9m.\)                            B. \(1,5m.\)

C. \(8,5cm.\)                           D. \(1,0cm.\)

Phương pháp giải:

Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha: \({d_2} - {d_1} = k\lambda \)

Lời giải chi tiết:

Bước sóng \(\lambda  = \dfrac{v}{f} = \dfrac{{75}}{{50}} = 1,5cm\)

Xét: \( - {S_1}{S_2} < k\lambda  < {S_1}{S_2}\\ \Leftrightarrow  - 10 < k.1,5 < 10 \\\Leftrightarrow  - 6,6 < k < 6,6\)

\( \Rightarrow k =  - 3;.....;3\)

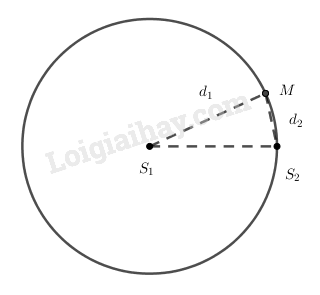
Do M là điểm mà phân tử tại đó dao động với biên độ cực đại cách điểm \({S_2}\)một đoạn ngắn nhất nên M thuộc đường cực đại \(k =  - 6\)

\( \Rightarrow M{S_2} - M{S_1} =  - 6\lambda \\ =  - 6.1,5 =  - 9\)

\(M{S_1} = {S_1}{S_2} = 10cm \Rightarrow M{S_2} = 1cm\)

Chọn D

II.9

Hai điểm \(M,N\) cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm khi li độ dao động của phần tử tại \(M\) là \(3cm\) thì li độ dao động của phần tử tại \(N\) là \( - 3cm\). Biên độ của sóng bằng

A. \(2\sqrt 3 cm.\)                      B. \(3\sqrt 2 cm.\)

C. \(3m.\)                              D. \(6cm.\)

Phương pháp giải:

Sử dụng vòng tròn lượng giác

Lời giải chi tiết:

Ta có: độ lệch pha giữa \(M\) và \(N\) là \(\Delta \varphi  = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi .\dfrac{\lambda }{3}}}{\lambda } = \dfrac{{2\pi }}{3}rad\)

Ta có vòng tròn lượng giác:

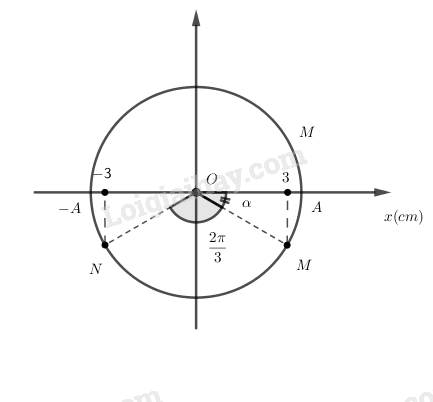
Từ hình vẽ: suy ra \(\alpha  =  - \dfrac{\pi }{6}rad\)

\({x_M} = A\cos ( - \dfrac{\pi }{6})\\ \Rightarrow A = \dfrac{{{x_M}}}{{\cos ( - \dfrac{\pi }{6})}} = \dfrac{3}{{\cos ( - \dfrac{\pi }{6})}} \\= 2\sqrt 3 cm\)

Chọn A