Bài II.15 trang 32 SBT Vật Lí 12
Giải bài II.15 trang 32 sách bài tập vật lí 12. Ở một chất lỏng có hai nguồn A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình là
Đề bài
Ở mặt chất lỏng có hai nguồn \(A,B\) cách nhau \(18cm\), dao động theo phương thẳng đứng với phương trình là \({u_A} = {u_B} = a{\rm{cos}}50\pi t.\) Tốc độ truyền sóng ở mặt chất lỏng là \(50cm/s.\) Gọi \(O\) là trung điểm của \(AB\), điểm \(M\) ở mặt chất lỏng nằm trên đường trung trực của \(AB\) và gần \(O\) nhất sao cho phần tử chất lỏng tại \(M\) dao động cùng pha với phần tử chất lỏng tại \(O\). Hỏi khoảng cách là bao nhiêu?
Phương pháp giải - Xem chi tiết
Sử dụng điều kiện cùng pha: \(d = k\lambda \)
Lời giải chi tiết
Tần số \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{50\pi }}{{2\pi }} = 25Hz\)
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{50}}{{25}} = 2cm\)
Độ lệch pha giữa nguồn và điểm cách nguồn một đoạn \(d\) là \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\), vậy tất cả các điểm thuộc đường tròn tâm \(A\) bán kính \(AO\) đều cùng pha với \(O\) \( \Rightarrow M'\) cùng pha với \(O\)
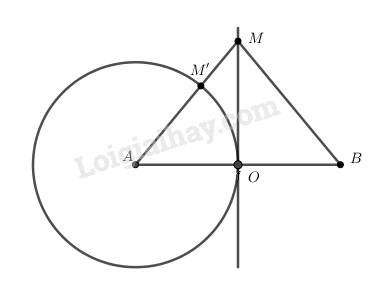
Để \(M\) là điểm gần\({\rm{O}}\)nhất, cùng pha với \({\rm{O}}\)thì \(M\) cùng pha với \(M'\), gần \(M'\)nhất \( \Rightarrow MM' = \lambda \)
\( \Rightarrow \) \(AM = AO + \lambda \)
\(\begin{array}{l}OM = \sqrt {A{M^2} - A{O^2}} \\ = \sqrt {{{(AO + \lambda )}^2} - A{O^2}} \\ = \sqrt {{{(9 + 2)}^2} - {9^2}} = 2\sqrt {10} cm\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài II.15 trang 32 SBT Vật Lí 12 timdapan.com"







