Bài 74 trang 169 SBT toán 9 tập 1
Giải bài 74 trang 169 sách bài tập toán 9. Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.
Đề bài
Cho hai đường tròn đồng tâm \(O.\) Một đường tròn \((O’)\) cắt một đường tròn tâm \(O\) tại \(A, B\) và cắt đường tròn tâm \(O\) còn lại tại \(C, D.\) Chứng minh rằng \(AB // CD.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tam là trung trực của dây chung.
Lời giải chi tiết
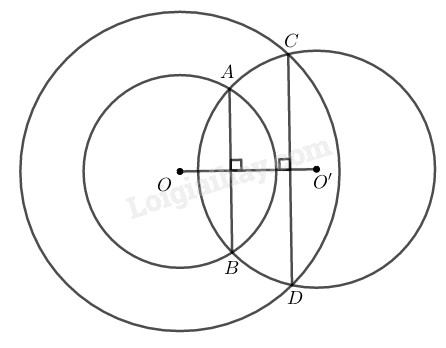
Vì đường tròn \((O’)\) cắt đường tròn \(( O; OA)\) tại \(A\) và \(B\) nên \(OO’\) là trung trực của \(AB\)
Suy ra: \(OO’ ⊥ AB\;\; (1)\)
Vì đường tròn \((O’) \) cắt đường tròn \((O; OC)\) tại \(C\) và \(D\) nên \(OO’\) là trung trực của \(CD\)
Suy ra: \(OO’ ⊥ CD \;\; (2)\)
Từ \((1)\) và \((2)\) suy ra: \(AB // CD.\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 74 trang 169 SBT toán 9 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 74 trang 169 SBT toán 9 tập 1 timdapan.com"







