Bài 71 trang 153 SBT toán 8 tập 2

Đề bài

Tính diện tích toàn phần của hình chóp cụt đều cho theo các kích thước trên hình \(154.\)

Lời giải chi tiết

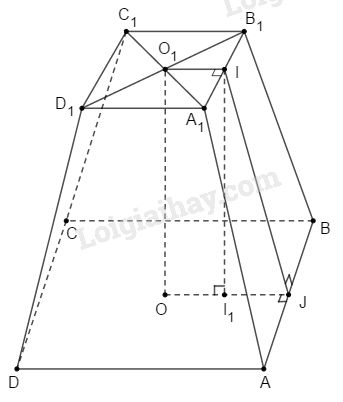
Ta có

\({A_1}{D_1} = 6\Rightarrow {O_1}I =6:2= 3\)

\(AD = 12 \Rightarrow {\rm O}J = 6\)

Kẻ \(I{I_1} ⊥ OJ\), ta có \(I_1J = 3\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(I{I_1}J\), ta có:

\(I{J^2} = I{I_1}^2 + {I_1}{J^2} = {9^2} + {3^2} = 90\)

\(IJ = \sqrt {90} \)

Diện tích một mặt  bên là:

\(\displaystyle S =S_{A_1B_1BA}={1 \over 2}.(A_1B_1+AB).IJ\)\(= \displaystyle {1 \over 2}\left( {6 + 12} \right).\sqrt {90}  = 9\sqrt {90} \) (đvdt)

Diện tích xung quanh bằng: \({S_{xq}}=4.S=4.9.\sqrt {90}  = 36\sqrt {90} \) (đvdt)

Diện tích đáy trên bằng: \(S_1 = 6.6 = 36\) (đvdt)

Diện tích đáy dưới bằng: \(S_2 = 12.12 = 144\) (đvdt)

Diện tích toàn phần của hình chóp cụt là:

\({S_{TP}} = S_{xq}+S_1+S_2=36\sqrt {90}  + 36 + 144\)\(\, = \left( {36\sqrt {90}  + 180} \right)\) (đvdt).