Giải bài 6 trang 92 SGK Toán 7 tập 2 - Cánh diều
Cho
Đề bài
Cho \(\Delta ABC = \Delta MNP\). Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.
Phương pháp giải - Xem chi tiết
Chứng minh tam giác ABD bằng tam giác MNQ.
Lời giải chi tiết
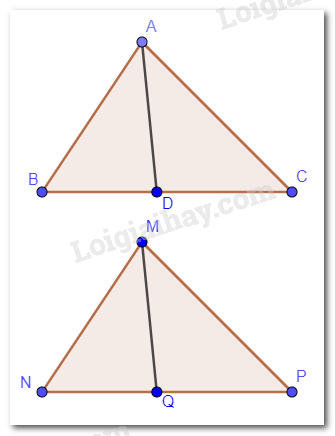
Ta có: \(\Delta ABC = \Delta MNP\) nên theo tính chất 2 tam giác bằng nhau, ta có:
\(\begin{array}{l}\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\\AB = MN,BC = NP,AC = NP.\end{array}\)
Mà AD và MQ lần lượt là phân giác của góc BAC và NMP nên \(\widehat {BAD} = \widehat {NMQ} = \dfrac{1}{2}\widehat {BAC} = \dfrac{1}{2}\widehat {NMP}\).
Xét hai tam giác ABD và MNQ có:
\(\widehat {BAD} = \widehat {NMQ}\);
AB = MN;
\(\widehat B = \widehat N\).
Vậy \(\Delta ABD = \Delta MNQ\) nên AD = MQ ( 2 cạnh tương ứng)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 6 trang 92 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







