Giải bài 52 trang 117 sách bài tập toán 11 - Cánh diều
Cho bốn điểm (A), (B), (C), (D) không cùng thuộc một mặt phẳng. Khẳng định nào sau đây là SAI?
Đề bài
Cho bốn điểm \(A\), \(B\), \(C\), \(D\) không cùng thuộc một mặt phẳng. Khẳng định nào sau đây là SAI?
A. Bốn điểm \(A\), \(B\), \(C\), \(D\) đã cho đôi một khác nhau.
B. Không có ba điểm nào trong bốn điểm \(A\), \(B\), \(C\), \(D\) thẳng hàng.
C. Hai đường thẳng \(AC\) và \(BD\) song song với nhau.
D. Hai đường thẳng \(AC\) và \(BD\) không có điểm chung với nhau.
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa và các tính chất của tứ diện.
Lời giải chi tiết
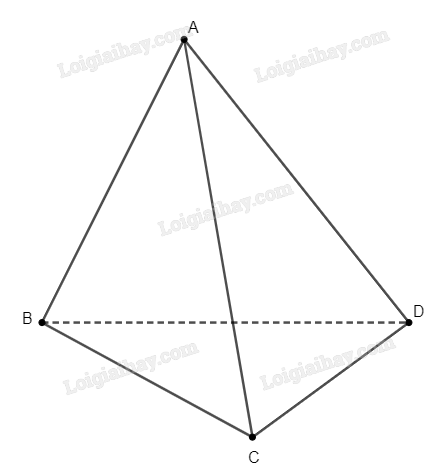
Đáp án A hiển nhiên đúng. Nếu có 2 điểm trùng nhau thì sẽ tồn tại một mặt phẳng chứa cả 4 điểm, do đó nó không phải là tứ diện.
Đáp án B đúng, do nếu tồn tại 3 điểm thẳng hàng thì sẽ tồn tại một mặt phẳng chứa đường thẳng đi qua 3 điểm thẳng hàng và điểm còn lại.
Đáp án C sai, do \(AC\) và \(BD\) không cùng nằm trong một mặt phẳng, nên chúng không thể song song với nhau.
Đáp án D đúng, do \(AC\) và \(BD\) là 2 đường thẳng chéo nhau.
Vậy đáp án cần chọn là C.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 52 trang 117 sách bài tập toán 11 - Cánh diều timdapan.com"







