Giải bài 5 (4.38) trang 79 vở thực hành Toán 7
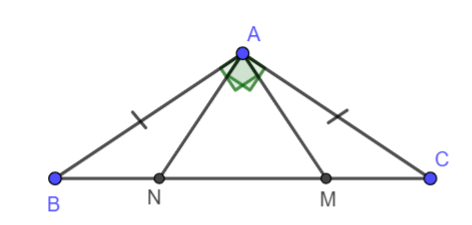
Bài 5 (4.38). Cho tam giác ABC cân tại đỉnh A có \(\widehat A = {120^o}\). Trên cạnh BC lấy điểm M, N sao cho MA, NA lần lượt vuông góc AB, AC. Chứng minh rằng a) \(\Delta BAM = \Delta CAN\) b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Đề bài
Bài 5 (4.38). Cho tam giác ABC cân tại đỉnh A có \(\widehat A = {120^o}\). Trên cạnh BC lấy điểm M, N sao cho MA, NA lần lượt vuông góc AB, AC. Chứng minh rằng
a) \(\Delta BAM = \Delta CAN\)
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Phương pháp giải - Xem chi tiết
Tam giác cân là tam giác có hai cạnh bằng nhau, hai góc ở đáy bằng nhau.
Lời giải chi tiết
|
GT |
\(\Delta ABC\)cân tại A,\(\widehat A = {120^o};M,N \in BC;\widehat {MAB} = \widehat {NAC} = {90^o}\) |
|
KL |
a) \(\Delta BAM = \Delta CAN\) b) Các tam giác ANB, AMC lần lượt cân tại N, M. |
a) Ta thấy hai tam giác BAM và CAN vuông tại M, N và có:
AB = AC, \(\widehat {ABM} = \widehat {ACN}\)( do \(\Delta ABC\)cân tại A).
Vậy \(\Delta BAM = \Delta CAN\) (cạnh góc vuông – góc nhọn).
b) Ta có \(\widehat B = \widehat C\) và \(\widehat A + \widehat B + \widehat C = {180^o}\). Suy ra \(\widehat B = \widehat C = \frac{{{{180}^o} - \widehat A}}{2} = {30^o}\)
Mặt khác \(\widehat {NAB} = \widehat {CAB} - \widehat {CAN} = {120^o} - {90^o} = {30^o} = \widehat {NBA}\)
Do đó \(\Delta ANB\) cân tại N. Tương tự ta có
\(\widehat {MAC} = \widehat {BAC} - \widehat {BAM} = {120^o} - {90^o} = {30^o} = \widehat {MCA}\)
Suy ra \(\Delta AMC\) cân tại M.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 5 (4.38) trang 79 vở thực hành Toán 7 timdapan.com"







