Bài 49 trang 96 SBT toán 8 tập 2
Giải bài 49 trang 96 sách bài tập toán 8. Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 9cm và 16cm...
Đề bài
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là \(9cm\) và \(16cm.\) Tính độ dài các cạnh của tam giác vuông đó (h.35)
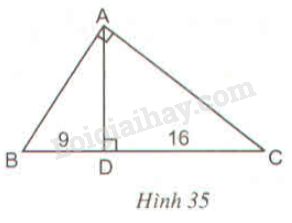
Phương pháp giải - Xem chi tiết
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Hai góc cùng phụ với một góc thứ ba thì bằng nhau.
- Định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải chi tiết
Xét hai tam giác vuông \(DAC\) và \(DBA\) có:
\(\widehat {ADC} = \widehat {BDA} = 90^\circ \)
\(\widehat {DCA} = \widehat {DAB}\) (hai góc cùng phụ với \(\widehat B\))
\( \Rightarrow ∆ DAC \backsim ∆ DBA\) (g.g)
\( \Rightarrow\displaystyle {{DB} \over {DA}} = {{DA} \over {DC}} \)
\( \Rightarrow D{A^2} = DB.DC\)
\( \Rightarrow DA = \sqrt {DB.DC} = \sqrt {9.16} = 12\)\(\; (cm)\).
Ta có: \(BC = BD + DC = 9 + 16 = 25\, (cm).\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(ABD\), ta có:
\( A{B^2} = D{A^2} + D{B^2} = {9^2} + {12^2} \)\(\,= 225\)
\(\Rightarrow AB = 15\,(cm) \)
Áp dụng định lí Pi-ta-go vào tam giác vuông \(ACD\), ta có:
\( A{C^2} = D{A^2} + D{C^2} = {12^2} + {16^2} \)\(\,= 400 \)
\(\Rightarrow AC = 20\,(cm) \).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 49 trang 96 SBT toán 8 tập 2 timdapan.com"







