Bài 4.4, 4.5, 4.6 phần bài tập bổ sung trang 44 SBT toán 7 tập 2
Giải bài 4.4, 4.5, 4.6 phần bài tập bổ sung trang 44 sách bài tập toán 7. Trong tam giác ABC, hai đường trung tuyến AA1 và BB1 cắt nhau tại điểm O. Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO bằng 5cm^2.
Bài 4.4
Trong tam giác \(ABC,\) hai đường trung tuyến \(\displaystyle {\rm{A}}{{\rm{A}}_1}\) và \(\displaystyle B{B_1}\) cắt nhau tại điểm \(O.\) Hãy tính diện tích tam giác \(ABC\) nếu diện tích tam giác \(ABO\) bằng \(\displaystyle 5c{m^2}\).
Phương pháp giải:
Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng \(\displaystyle \dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Sử dụng: Nếu hai tam giác có cùng chiều cao thì tỉ số diện tích sẽ bằng với tỉ số hai cạnh đáy tương ứng.
Lời giải chi tiết:
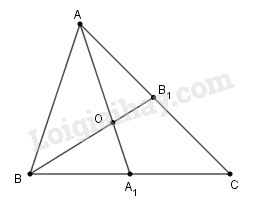
Vì tam giác \(\displaystyle ABC\) có hai đường trung tuyến \(\displaystyle {\rm{A}}{{\rm{A}}_1}\) và \(\displaystyle B{B_1}\) cắt nhau tại điểm \(\displaystyle O\) nên \(\displaystyle O\) là trọng tâm tam giác \(\displaystyle ABC,\) suy ra \(\displaystyle {\rm{A}}O = {2 \over 3}{\rm{A}}{{\rm{A}}_1}.\)
Ta có:
\(\displaystyle {S_{AOB}} = {2 \over 3}{S_{{\rm{A}}{{\rm{A}}_1}B}}\) (vì có cùng chiều cao hạ từ \(\displaystyle B\) và \(\displaystyle {\rm{A}}O = {2 \over 3}{\rm{A}}{{\rm{A}}_1}\))
Suy ra \(\displaystyle {S_{AA_1B}} = {2 \over 3}{S_{AOB}}\)
Lại có \(\displaystyle {{\rm{S}}_{AB{A_1}}} = {1 \over 2}{S_{ABC}}\) (vì có cùng chiều cao hạ từ \(\displaystyle A\) và \(\displaystyle B{A_1} = {1 \over 2}BC\)) ;
Từ đó suy ra \(\displaystyle {{\rm{S}}_{ABC}} = 2{{\rm{S}}_{AB{A_1}}}\)\(\displaystyle =2.\dfrac{3}{2}{{\rm{S}}_{AOB}} = 3{{\rm{S}}_{AOB}}\)
Nếu \(\displaystyle {{\rm{S}}_{AOB}} = 5c{m^2}\) thì \(\displaystyle {S_{ABC}} = 3.5 = 15\left( {c{m^2}} \right)\)
Bài 4.5
Chứng minh rằng các trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng (đôi một) bằng nhau.
Phương pháp giải:
Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng \(\displaystyle \dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Sử dụng: Nếu hai tam giác có cùng chiều cao thì tỉ số diện tích sẽ bằng với tỉ số hai cạnh đáy tương ứng.
Lời giải chi tiết:
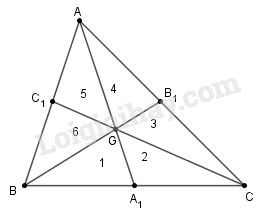
Xét tam giác \(ABC\) có ba đường trung tuyến \(AA_1, BB_1, CC_1\) cắt nhau tại trọng tâm \(G.\)
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Tương tự bài 4.4 ta có:
+) Vì tam giác \(\displaystyle ABC\) có \(\displaystyle G\) là trọng tâm tam giác \(\displaystyle ABC,\) suy ra \(\displaystyle {\rm{A}}G = {2 \over 3}{\rm{A}}{{\rm{A}}_1}.\)
Ta có:
\(\displaystyle {S_{AGB}} = {2 \over 3}{S_{{\rm{A}}{{\rm{A}}_1}B}}\) (vì có cùng chiều cao hạ từ \(\displaystyle B\) và \(\displaystyle {\rm{A}}G = {2 \over 3}{\rm{A}}{{\rm{A}}_1}\))
Suy ra \(\displaystyle {S_{AA_1B}} = {2 \over 3}{S_{AGB}}\)
Lại có \(\displaystyle {{\rm{S}}_{AB{A_1}}} = {1 \over 2}{S_{ABC}}\) (vì có cùng chiều cao hạ từ \(\displaystyle A\) và \(\displaystyle B{A_1} = {1 \over 2}BC\)) ;
Từ đó suy ra \(\displaystyle {{\rm{S}}_{ABC}} = 2{{\rm{S}}_{AB{A_1}}}\)\(\displaystyle =2.\dfrac{3}{2}{{\rm{S}}_{AGB}} = 3{{\rm{S}}_{AGB}}\) nên \({{\rm{S}}_{AGB}}=\dfrac{1}{3}S_{ABC}\) (1)
+) Vì G là trọng tâm tam giác ABC nên \(CG = \dfrac{2}{3}C{C_1}\)
Ta có: \({S_{BGC}} = \dfrac{2}{3}{S_{BC{C_1}}}\) (vì có cùng chiều cao kẻ từ B đến \(C{C_1}\) và cạnh đáy \(CG = \dfrac{2}{3}C{C_1}\))
Mà \({S_{BC{C_1}}} = \dfrac{1}{2}{S_{BAC}}\) (vì có cùng chiều cao kẻ từ C đến AB và cạnh đáy \(B{C_1} = \dfrac{1}{2}AB\))
Suy ra \({S_{BGC}} = \dfrac{2}{3}{S_{BC{C_1}}} = \dfrac{2}{3}.\dfrac{1}{2}{S_{ABC}} = \dfrac{1}{3}{S_{ABC}}\), hay \({S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\) (2)
Ta có: \({S_{AGC}} = \dfrac{2}{3}{S_{AC{C_1}}}\) (vì có cùng chiều cao kẻ từ A đến \(C{C_1}\) và cạnh đáy \(CG = \dfrac{2}{3}C{C_1}\))
Mà \({S_{AC{C_1}}} = \dfrac{1}{2}{S_{BAC}}\) (vì có cùng chiều cao kẻ từ C đến AB và cạnh đáy \(A{C_1} = \dfrac{1}{2}AB\))
Suy ra \({S_{AGC}} = \dfrac{2}{3}{S_{AC{C_1}}} = \dfrac{2}{3}.\dfrac{1}{2}{S_{ABC}} = \dfrac{1}{3}{S_{ABC}}\), hay \({S_{GAC}} = \dfrac{1}{3}{S_{ABC}}\) (3)
Từ (1), (2) và (3) suy ra: \(\displaystyle {S_{GAB}} = {S_{GBC}} = {S_{GCA}} = {1 \over 3}{S_{ABC}}\)
Ta lại có \({{\rm{S}}_1} = {S_2},{S_3} = {S_4},{S_5} = {S_6}\) (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau)
Vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau.
Bài 4.6
Cho tam giác \(\displaystyle ABC\) với đường trung tuyến \(\displaystyle D.\) Trên tia \(\displaystyle AD\) lấy điểm \(\displaystyle E\) sao cho \(\displaystyle AD = DE,\) trên tia \(\displaystyle BC\) lấy điểm \(\displaystyle M\) sao cho \(\displaystyle BC = CM.\)
a) Tìm trọng tâm của tam giác \(\displaystyle AEM.\)
b) So sánh các cạnh của tam giác \(\displaystyle ABC\) với các đường trung tuyến của tam giác \(\displaystyle AEM\)
c) So sánh các đường trung tuyến của tam giác \(\displaystyle ABC\) với các cạnh của tam giác \(\displaystyle AEM.\)
Phương pháp giải:
Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng \(\displaystyle \displaystyle \dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Sử dụng tính chất hai tam giác bằng nhau.
Lời giải chi tiết:
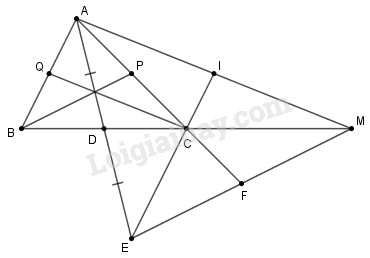
a) Do \(\displaystyle AD = DE\) nên \(\displaystyle MD\) là một đường trung tuyến của tam giác \(\displaystyle AEM.\)
Hơn nữa do \(\displaystyle C{\rm{D}} = {1 \over 2}CB = {1 \over 2}CM\)
Nên \(\displaystyle M{\rm{D}} =CD+CM= {1 \over 2}CM+CM = {3 \over 2}CM\)
Suy ra \(\displaystyle MC=\dfrac{2}{3}MD\)
Nên \(\displaystyle C\) là trọng tâm của tam giác \(\displaystyle AEM.\)
b) Các đường thẳng \(\displaystyle AC, EC\) lần lượt cắt \(\displaystyle EM, AM\) tại \(\displaystyle F, I.\) Tam giác \(\displaystyle AEM\) có các đường trung tuyến là \(\displaystyle AF, EI, MD.\)
Xét \(∆ADB\) và \( ∆EDC\) có:
+) \(BD=DC\) (vì AD là đường trung tuyến của tam giác \(\displaystyle ABC)\)
+) \(\widehat{BDA}=\widehat{CDE}\) (hai góc đối đỉnh)
+) \(AD=DE\) (gt)
Ta có \(\displaystyle ∆ADB = ∆EDC\) (c.g.c) nên \(\displaystyle AB = EC\)
Mà \(C\) là trọng tâm của tam giác \(\displaystyle AEM\) (câu a) nên \(\displaystyle AC = {2 \over 3}{\rm{AF;BC = CM = }}{2 \over 3}{\rm{MD}};\)\(\displaystyle AB = EC = {2 \over 3}EI\)
c) Trước tiên, theo giả thiết, ta có \(\displaystyle AD = DE\) nên \(\displaystyle A{\rm{D}} = {1 \over 2}A{\rm{E}}\)
Gọi \(\displaystyle BP, CQ\) là các trung tuyến của \(\displaystyle ∆ABC.\)
Lại có: \(\displaystyle ∆BCP = ∆MCF\) (c-g-c) (do \( CP=CF=\dfrac {1}{2}AC, BC=CM, \) \(\displaystyle \widehat {PCB}=\widehat {FCM}\) (đối đỉnh))
\(\displaystyle \Rightarrow BP = FM = {1 \over 2}EM\).
Ta sẽ chứng minh \(\displaystyle CQ = {1 \over 2}AM\)
Ta có:
\(\displaystyle \eqalign{
& \Delta AB{\rm{D}} = \Delta EC{\rm{D}} (c-g-c)\cr
&\Rightarrow \widehat {BA{\rm{D}}} = \widehat {CED} \cr
& \Rightarrow AB//EC \Rightarrow \widehat {QAC} = \widehat {IC{\rm{A}}} \cr} \)
Hai tam giác \(\displaystyle ACQ\) và \(\displaystyle CAI\) có cạnh \(\displaystyle AC\) chung, \(\displaystyle \widehat {QAC} = \widehat {IC{\rm{A}}}\);
\(\displaystyle AQ = {1 \over 2}AB = {1 \over 2}EC = IC\) nên chúng bằng nhau.
Vậy \(\displaystyle CQ = AI = {1 \over 2}AM\).
Tóm lại: \(\displaystyle A{\rm{D}} = {1 \over 2}A{\rm{E,BP = }}{1 \over 2}{\rm{EM, }}\)\(\displaystyle CQ={1 \over 2}{\rm{AM}}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4.4, 4.5, 4.6 phần bài tập bổ sung trang 44 SBT toán 7 tập 2 timdapan.com"







