Bài 32 trang 42 SBT toán 7 tập 2
Giải bài 32 trang 42 sách bài tập toán 7. Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Đề bài
Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Sử dụng tính chất hai tam giác bằng nhau.
Lời giải chi tiết
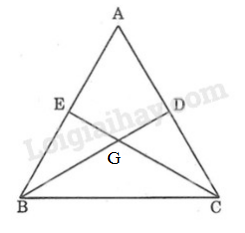
Giả sử \(∆ABC\) có hai đường trung tuyến \(BD, CE \) và \(BD = CE.\) Gọi \(G\) là giao điểm \(BD\) và \(CE.\)
Khi đó, G là trọng tâm của tam giác ABC. Suy ra:
\(\displaystyle BG = {2 \over 3}B{\rm{D}}\) (tính chất đường trung tuyến)
\(\displaystyle CG = {2 \over 3}CE\) (tính chất đường trung tuyến)
Mà \(BD = CE\)
Suy ra: \(BG = CG\)
\( \Rightarrow BG + GD = CG + GE\)
\( \Rightarrow GD = GE\)
Xét \(∆BGE\) và \(∆CGD:\)
+) \(BG = CG\) (chứng minh trên)
+) \(\widehat {BGE} = \widehat {CG{\rm{D}}}\) (đối đỉnh)
+) \(GE = GD\) (chứng minh trên)
Do đó: \(∆BGE = ∆CGD\) (c.g.c)
\( \Rightarrow BE = CD\) (1)
\(\displaystyle BE = {1 \over 2}AB\) (vì \(E\) là trung điểm \(AB)\) (2)
\(\displaystyle C{\rm{D = }}{1 \over 2}AC\) (vì \(D\) là trung điểm \(AC) \) (3)
Từ (1), (2) và (3) suy ra: \(AB = AC.\)
Vậy \(∆ABC\) cân tại \(A.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 32 trang 42 SBT toán 7 tập 2 timdapan.com"