Giải bài 4.38 trang 66 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

Đề bài

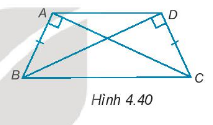
Cho 4 điểm A, B, C, D như hình 4.40 trong đó AB = DC. Chứng minh rằng:

a) AC = BD

b) \(AD\parallel BC\)

Lời giải chi tiết

Xét \(\Delta ABC\) và \(\Delta DCB\) có:

AB = DC (gt)

BC: Cạnh chung

\(\begin{array}{l}\widehat {BAC} = \widehat {CDB} = {90^0}\\ \Rightarrow \Delta ABC = \Delta DCB\left( {ch - cgv} \right)\\ \Rightarrow AC = DB\left( {ctu} \right)\end{array}\)

b)

Ta có: \(\Delta ABC = \Delta DCB\left( {cmt} \right) \Rightarrow \left\{ \begin{array}{l}\widehat {ACB} = \widehat {DBC}\\\widehat {ABC} = \widehat {DCB}\end{array} \right.\)

Lại có:\(\left\{ \begin{array}{l}\widehat {ABD} = \widehat {ABC} - \widehat {DBC}\\\widehat {DCA} = \widehat {DCB} - \widehat {ACB}\end{array} \right. \Rightarrow \widehat {ABD} = \widehat {DCA}\).

Xét \(\Delta ABD\) và \(\Delta ACD\) có:

BA = CD (gt)

BD = CA

\(\begin{array}{l}\widehat {ABD} = \widehat {DCA}\left( {cmt} \right)\\ \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right)\\ \Rightarrow \widehat {ADB} = \widehat {DAC}\end{array}\)

Nếu gọi E là giao điểm của AC và BD thì ta có:

\(\begin{array}{l}\widehat {ADB} = \dfrac{{\widehat {ADB} + \widehat {DAC}}}{2} = \dfrac{{\widehat {ADE} + \widehat {DAE}}}{2} = \dfrac{{{{180}^0} - \widehat {AED}}}{2} = \dfrac{{{{180}^0} - \widehat {BEC}}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\widehat {EBC} + \widehat {ECB}}}{2} = \dfrac{{\widehat {ACB} + \widehat {DBC}}}{2} = \widehat {DBC}\end{array}\)

Mà 2 góc ở vị trí so le trong 

Nên \(AD\parallel BC\). ( Dấu hiệu nhận biết 2 đường thẳng song song)