Giải bài 4 trang 71 vở thực hành Toán 7
Bài 4. Cho hình vẽ bên. Biết \(\widehat {DAC} = \widehat {CBD} = {90^o},AD = BC\), hãy chứng minh rằng \(\widehat {BAD} = \widehat {ABC}\).
Đề bài
Bài 4. Cho hình vẽ bên. Biết \(\widehat {DAC} = \widehat {CBD} = {90^o},AD = BC\), hãy chứng minh rằng \(\widehat {BAD} = \widehat {ABC}\).
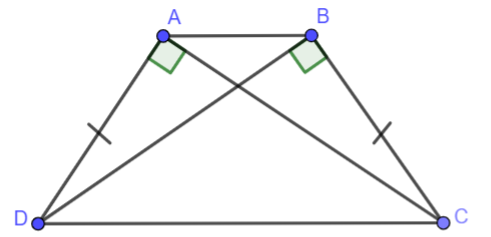
Phương pháp giải - Xem chi tiết
Chứng minh tam giác BAD và ABC bằng nhau.
Lời giải chi tiết
Ta thấy hai tam giác ADC và BCD lần lượt vuông góc tại các đỉnh A, B và có:
DC là cạnh chung
AD = BC (theo giả thiết)
Vậy \(\Delta ADC = \Delta BCD\)(cạnh huyền – cạnh góc vuông). Từ đây suy ra AC = BD.
Hai tam giác BAD và ABC có: AD = BC (theo giả thiết), AB là cạnh chung, BD = AC (theo chứng minh trên). Vậy \(\Delta BAD = \Delta ABC\)(hai cạnh góc vuông).
Suy ra \(\widehat {BAD} = \widehat {ABC}\).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 71 vở thực hành Toán 7 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 71 vở thực hành Toán 7 timdapan.com"







