Bài 38 trang 162 SBT toán 9 tập 1
Giải bài 38 trang 162 sách bài tập toán 9. Cho đường tròn (O) bán kính bằng 2cm. Một đường thẳng đi qua điểm A nằm bên ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ đường kính COD. Tính độ dài AD.
Đề bài
Cho đường tròn \((O)\) bán kính bằng \(2cm.\) Một đường thẳng đi qua điểm \(A\) nằm bên ngoài đường tròn và cắt đường tròn tại \(B\) và \(C,\) trong đó \(AB = BC.\) Kẻ đường kính \(COD.\) Tính độ dài \(AD.\)
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
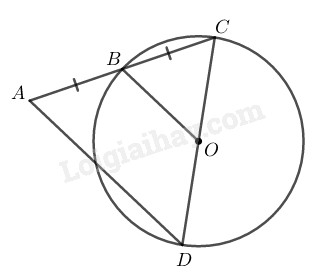
Trong tam giác \(ACD,\) ta có:
+) \(B\) là trung điểm của \(AC\;\; (gt)\)
+) \(O\) là trung điểm của \(CD\)
Nên \(OB\) là đường trung bình của \(∆ACD.\)
Suy ra: \(OB = \displaystyle{1 \over 2}AD\) ( tính chất đường trung bình của tam giác)
Vậy \(AD = 2. OB = 2.2 = 4 (cm).\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 38 trang 162 SBT toán 9 tập 1 timdapan.com"







