Bài 3.50 trang 163 SBT hình học 11

Đề bài

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy.

a) Chứng minh tam giác SBC vuông

b) Gọi H là chân đường cao vẽ từ B của tam giác ABC.

Chứng minh (SAC) ⊥ (SBH)

c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)

Lời giải chi tiết

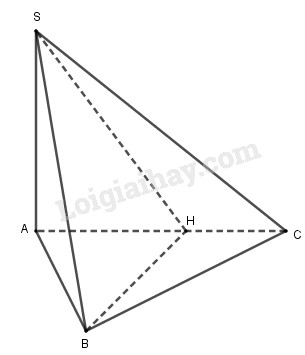
a) Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)

Mà \(BC \bot AB\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)

\( \Rightarrow \Delta SBC\) vuông tại B.

b) Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BH\)

Mà \(BH \bot AC\) nên \(BH \bot \left( {SAC} \right)\)

Lại có \(\left\{ \begin{array}{l}BH \subset \left( {SBH} \right)\\BH \bot \left( {SAC} \right)\end{array} \right. \Rightarrow \left( {SBH} \right) \bot \left( {SAC} \right)\)

c) Do \(BH \bot \left( {SAC} \right)\) nên \(d\left( {B,\left( {SAC} \right)} \right) = BH\).

Tam giác \(ABC\) vuông tại B đường cao BH nên:

\(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{A^2}}} + \dfrac{1}{{B{C^2}}}\) \( = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}}\) \( \Rightarrow B{H^2} = \dfrac{{4{a^2}}}{5}\) \( \Rightarrow BH = \dfrac{{2a}}{{\sqrt 5 }} = \dfrac{{2a\sqrt 5 }}{5}\)